题目内容
 已知反比例函数y=
已知反比例函数y=| m-8 |
| x |
(1)求m的值;
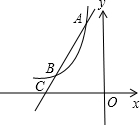
(2)如图,过点A作直线AC与函数y=
| m-8 |
| x |
(3)连接OA、OB,求△AOB的面积.
分析:(1)将点A(-1,6)代入反比例函数y=
,即可求出m的值.
(2)由A,C两点的坐标,可得出B的坐标,根据两点间的距离公式可分别算出AB,和BC的长,即可得出结论.
(3)要求△AOB的面积,根据三角形的面积公式,已知AB的长,求出原点到直线AB的距离即可.
| m-8 |
| x |
(2)由A,C两点的坐标,可得出B的坐标,根据两点间的距离公式可分别算出AB,和BC的长,即可得出结论.
(3)要求△AOB的面积,根据三角形的面积公式,已知AB的长,求出原点到直线AB的距离即可.
解答: (1)解:将点A(-1,6)代入反比例函数y=
(1)解:将点A(-1,6)代入反比例函数y=
,
6=
,解得m=2.
(2)证明:已知A,C两点的坐标,C(-4,0),A(-1,6),
∴直线AC解析式为y=2x+8,易求得B(-3,2),
∴AB=
=
=2
,
BC=
=
,
∴AB=2BC.
(3)解:已知A,B坐标,则可得直线AB的方程为:y=2x+b,
将A点代入所设方程可得b=8,
∴y=2x+8,则原点到直线AB的距离d=
,
∴△AOB的面积=
•AB•d=8.
 (1)解:将点A(-1,6)代入反比例函数y=
(1)解:将点A(-1,6)代入反比例函数y=| m-8 |
| x |
6=
| m-8 |
| -1 |
(2)证明:已知A,C两点的坐标,C(-4,0),A(-1,6),
∴直线AC解析式为y=2x+8,易求得B(-3,2),
∴AB=
| (-1+3)2+(6-2)2 |
| 20 |
| 5 |
BC=
| (-4+3)2+(0-2)2 |
| 5 |
∴AB=2BC.
(3)解:已知A,B坐标,则可得直线AB的方程为:y=2x+b,
将A点代入所设方程可得b=8,
∴y=2x+8,则原点到直线AB的距离d=
8
| ||
| 5 |
∴△AOB的面积=
| 1 |
| 2 |
点评:本题考查了二次反比例函数的应用和三角形的面积公式,比较综合,难度较大,适合作为试卷的压轴题.

练习册系列答案
相关题目
 面积为3,若直线y=ax+b经过点A,并且经过反比例函数
面积为3,若直线y=ax+b经过点A,并且经过反比例函数 已知反比例函数
已知反比例函数