题目内容
(2009•柳州)某校积极推进“阳光体育”工程,本学期在九年级11个班中开展篮球单循环比赛(每个班与其它班分别进行一场比赛,每班需进行10场比赛).比赛规则规定:每场比赛都要分出胜负,胜一场得3分,负一场得-1分.(1)如果某班在所有的比赛中只得14分,那么该班胜负场数分别是多少?
(2)假设比赛结束后,甲班得分是乙班的3倍,甲班获胜的场数不超过5场,且甲班获胜的场数多于乙班,请你求出甲班、乙班各胜了几场.
【答案】分析:(1)设该班胜x场,则该班负(10-x)场.根据得分列方程求解;
(2)设甲班胜了x场,乙班胜了y场,根据甲班得分是乙班的3倍,用x表示y.再根据甲班获胜的场数不超过5场,且甲班获胜的场数多于乙班,列出不等式组求解.
解答:解:(1)设该班胜x场,则该班负(10-x)场.
依题意得3x-(10-x)=14
解之得x=6(3分)
所以该班胜6场,负4场;
(2)设甲班胜了x场,乙班胜了y场,依题意有:
3x-(10-x)=3[3y-(10-y)],
化简,得3y=x+5,
即y=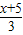 .
.
由于x,y是非负整数,且0≤x≤5,x>y,
∴x=4,y=3.
所以甲班胜4场,乙班胜3场.
答:(1)该班胜6场,负4场.(2)甲班胜4场,乙班胜3场.
点评:此题主要是根据得分列方程求解.在(2)中列不等式组求得x,y的取值范围求解.
(2)设甲班胜了x场,乙班胜了y场,根据甲班得分是乙班的3倍,用x表示y.再根据甲班获胜的场数不超过5场,且甲班获胜的场数多于乙班,列出不等式组求解.
解答:解:(1)设该班胜x场,则该班负(10-x)场.
依题意得3x-(10-x)=14
解之得x=6(3分)
所以该班胜6场,负4场;
(2)设甲班胜了x场,乙班胜了y场,依题意有:
3x-(10-x)=3[3y-(10-y)],
化简,得3y=x+5,
即y=
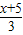 .
.由于x,y是非负整数,且0≤x≤5,x>y,
∴x=4,y=3.
所以甲班胜4场,乙班胜3场.
答:(1)该班胜6场,负4场.(2)甲班胜4场,乙班胜3场.
点评:此题主要是根据得分列方程求解.在(2)中列不等式组求得x,y的取值范围求解.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目