题目内容
如图2,四边形ABCD中,E是BC的中点,连结DE并延长,交AB的延长线
于点F,AB=BF.添加一个条件,使四边形ABCD是平行四边形.下列条件中正确的是( )

于点F,AB=BF.添加一个条件,使四边形ABCD是平行四边形.下列条件中正确的是( )
| A.AD=BC | B.CD=BF | C.∠F=∠CDE | D.∠A=∠C |

C
选择C:∠CDE=∠F,根据内错角相等,两直线平行可得CD∥BF,然后利用“角角边”证明△DEC和△BEF全等,根据全等三角形对应边相等可得CD=BF,然后求出CD=AB,根据一组对边平行且相等的四边形是平行四边形即可证明.
证明:∵∠CDE=∠F,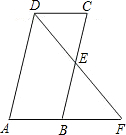
∴CD∥BF,
又∵E是BC的中点,
∴EC=EB,
在△DEC和△BEF中,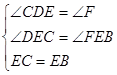 ,
,
∴△DEC≌△BEF(AAS),
∴CD=BF,
∵AB=BF,
∴AB∥CD且AB=CD,
∴四边形ABCD是平行四边形.
所以应选C。
本题考查了平行四边形的判定,两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;一组对边平行,一组对角相等的四边形是平行四边形.
证明:∵∠CDE=∠F,

∴CD∥BF,
又∵E是BC的中点,
∴EC=EB,
在△DEC和△BEF中,
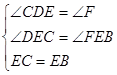 ,
,∴△DEC≌△BEF(AAS),
∴CD=BF,
∵AB=BF,
∴AB∥CD且AB=CD,
∴四边形ABCD是平行四边形.
所以应选C。
本题考查了平行四边形的判定,两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;一组对边平行,一组对角相等的四边形是平行四边形.

练习册系列答案
相关题目

 ,E是DC上一点,且BE = BC,则DE的长为
,E是DC上一点,且BE = BC,则DE的长为



 CD中,AD=4,BC=9,∠
CD中,AD=4,BC=9,∠