题目内容
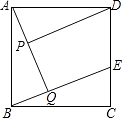
【题目】如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.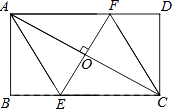
(1)求证:四边形AECF是菱形;
(2)若AB= ![]() ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
【答案】
(1)证明:∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
 ,
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形
(2)解:∵四边形ABCD是矩形,
∴CD=AB= ![]() ,
,
在Rt△CDF中,cos∠DCF= ![]() ,∠DCF=30°,
,∠DCF=30°,
∴CF= ![]() =2,
=2,
∵四边形AECF是菱形,
∴CE=CF=2,
∴四边形AECF是的面积为:ECAB=2 ![]()
【解析】(1)首先根据线段垂直平分线的性质得到AF=CF,AE=CE,OA=OC,然后再证明△AOF≌△COE,则可得AF=CE,从而可得到四边形的四条边都相等,故此可作出判断;
(2)由四边形ABCD是矩形,易求得CD的长,然后利用三角函数求得CF的长,最后依据菱形的面积=底×高求解即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目