题目内容
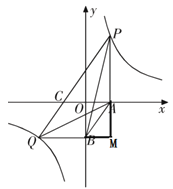
【题目】如图,P,Q分别是双曲线![]() 在第一、三象限上的点,PA⊥
在第一、三象限上的点,PA⊥![]() 轴,QB⊥
轴,QB⊥![]() 轴,垂足分别为A,B,点C是PQ与
轴,垂足分别为A,B,点C是PQ与![]() 轴的交点.设△PAB的面积为
轴的交点.设△PAB的面积为![]() ,△QAB的面积为
,△QAB的面积为![]() ,△QAC的面积为
,△QAC的面积为![]() ,则有( )
,则有( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】试题分析:如图,延长PA、QB交于点M,则△QMB是直角三角形,,可得AM=OB,BM=OA,根据反比例函数k的几何意义可得OB·BQ=OA·AP=k,所以AM·BQ=BM·AP,即![]() ,即可得
,即可得![]() ,由相似三角形的判定定理可得△ABM∽△PQM,根据相似三角形的性质可得∠BAM=∠QPM,所以AB∥PQ,即可得四边形ABQC是平行四边形,所以△QAB的面积等于△QAC的面积,即
,由相似三角形的判定定理可得△ABM∽△PQM,根据相似三角形的性质可得∠BAM=∠QPM,所以AB∥PQ,即可得四边形ABQC是平行四边形,所以△QAB的面积等于△QAC的面积,即![]() =
=![]() ,因AB∥PQ,根据同底等高的两个三角形的面积相等可得设△PAB的面积等于△QAB的面积,即
,因AB∥PQ,根据同底等高的两个三角形的面积相等可得设△PAB的面积等于△QAB的面积,即![]() =
=![]() ,所以
,所以![]() ,故选D.
,故选D.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
【题目】小丽妈妈在网上做淘宝生意,专门销售女式鞋子,一次,小丽发现一个进货单上的一个信息是:A款鞋的进价比B款鞋进价多20元,花500元进A款鞋的数量和花400元进B款鞋的数量相同.
(1)问A、B款鞋的进价分别是多少元?
(2)小丽在销售单上记录了两天的数据如表:
日期 | A款女鞋销量 | B款女鞋销量 | 销售总额 |
6月1日 | 12双 | 8双 | 2240元 |
6月2日 | 8双 | 10双 | 1960元 |
请问两种鞋的销售价分别是多少?
(3)小丽妈妈说:“两款鞋的利润率相同”,请通过计算,结合(1)(2)所给信息,判断小丽妈妈的说法是否正确,如果正确,请说明理由;如果错误,能否只调整其中一款的售价,使得两款鞋的利润率相同?能否同时调整两款的售价,使得两款鞋的利润率相同?请说明理由.