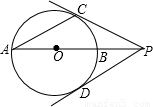
题目内容
如图,PA是⊙O的割线,且经过圆心O,与⊙O交于B、A两点,PD切⊙O于点D,AC是⊙O的一条弦,连结PC,且PC=PD.(1)求证:PC是⊙O的切线;(2)若AC=PD,连结BC.求证:AB=2BC
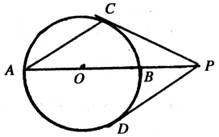
【答案】
(1)连结OC、OD
在△POC和△POD中,∵OC=OD,PC=PD,PO=PO, ∴△POC≌△POD
∴∠ODP=∠OCP.
∵PD是⊙O的切线,∴∠ODP=90°,∴∠OCP=90°.
∴PC是⊙O的切线.
(2)∵PC、PD是⊙O的两条切线,
∴PC=PD,
又∵AC=PD
∴AC=PC.
∴∠A=∠CPA
设∠A=x,则∠COP=2x,∠CPA=x.在Rt△POC中,2x+x+90°=180°,
∴x=30°.即∠A=30°.
又∵△ABC是Rt△,
∴AB=2BC
【解析】(1)要证PC是⊙O的切线,只要连接OC,OD,通过证明△OCP≌△ODP得出∠OCP=90°即可.
(2)利用直角三角形POC内角和为180°算出∠CPA的度数,从而得出∠A的度数,再根据Rt△ABC的边角关系得出结论。

练习册系列答案
相关题目
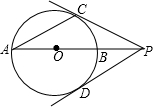 如图,PA是⊙O的割线,且经过圆心O,与⊙O交于B、A两点,PD切⊙O于点D,AC是⊙O的一条弦,连结PC,且PC=PD.
如图,PA是⊙O的割线,且经过圆心O,与⊙O交于B、A两点,PD切⊙O于点D,AC是⊙O的一条弦,连结PC,且PC=PD.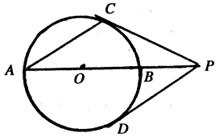
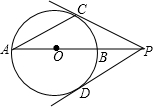 如图,PA是⊙O的割线,且经过圆心O,与⊙O交于B、A两点,PD切⊙O于点D,AC是⊙O的一条弦,连结PC,且PC=PD.
如图,PA是⊙O的割线,且经过圆心O,与⊙O交于B、A两点,PD切⊙O于点D,AC是⊙O的一条弦,连结PC,且PC=PD.