题目内容
已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
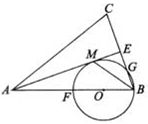
(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=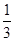 时,求⊙O的半径.
时,求⊙O的半径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=
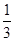 时,求⊙O的半径.
时,求⊙O的半径. (1)通过证明OM⊥AE即可证明AE与⊙O相切。
(2)半径为
(2)半径为

试题分析:(1)证明:连接OM,则OM=OB
∴∠1=∠2

∵BM平分∠ABC
∴∠1=∠3
∴∠2=∠3
∴OM∥BC
∴∠AMO=∠AEB
在△ABC中,AB=AC,AE是角平分线
∴AE⊥BC
∴∠AEB=90°
∴∠AMO=90°
∴OM⊥AE
∵点M在圆O上,
∴AE与⊙O相切;
(2)解:在△ABC中,AB=AC,AE是角平分线
∴BE=
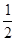 BC,∠ABC=∠C
BC,∠ABC=∠C∵BC=4,cos C=

∴BE=2,cos∠ABC=

在△ABE中,∠AEB=90°
∴AB=
 =6
=6设⊙O的半径为r,则AO=6-r
∵OM∥BC
∴△AOM∽△ABE
∴
 =
=
∴
 =
=
解得r=

∴⊙O的半径为

点评:此题是综合题,考查等腰三角形,平行线,角平分线,直线和圆的位置关系,相似三角形等知识点

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
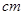 ,面积为32
,面积为32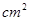 ,则△ABC的内切圆半径为____________.
,则△ABC的内切圆半径为____________.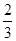 ,∠A=30º.
,∠A=30º.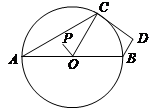
 的长;
的长;



 ;,求AB的长.
;,求AB的长.