题目内容
【题目】如图,在平面直角坐标系中,点A(-4,0),点B(0,-5),点C(m,0)(m>0),过点A作直线BC的垂线交y轴于点D,则随着m值的增大,经过A,D,C三点的抛物线的开口大小的变化情况是( )
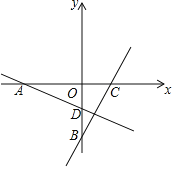
A.保持不变B.逐渐变大C.逐渐变小D.时大时小
【答案】A
【解析】
设OD=n,首先易证△OAD∽△OBC,列出比例式求出n=![]() ,即可得到点D坐标,然后设经过A,D,C三点的抛物线的解析式为y=a(x+4)(x﹣m),将点D坐标代入可求出a=
,即可得到点D坐标,然后设经过A,D,C三点的抛物线的解析式为y=a(x+4)(x﹣m),将点D坐标代入可求出a=![]() ,问题得解.
,问题得解.
设OD=n,
∵点A(﹣4,0),点B(0,﹣5).点C(m,0)(m>0),
∴OA=4,OB=5,OC=m,
∵AD⊥BC,
∴∠OAD=∠DBC,
∴△OAD∽△OBC,
∴![]() =
=![]() ,
,
∴![]() ,
,
∴n=![]() ,
,
∴D(0,![]() ),
),
设经过A,D,C三点的抛物线的解析式为y=a(x+4)(x﹣m),
将D(0,![]() )代入可得:
)代入可得:![]() =﹣4ma,
=﹣4ma,
∴a=![]() ,
,
∴抛物线对的解析式为:y=![]() (x+4)(x﹣m),
(x+4)(x﹣m),
由于抛物线的二次项系数为![]() ,
,
∴经过A,D,C三点的抛物线的开口大小不变,
故选:A.

练习册系列答案
相关题目