��Ŀ����
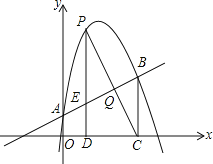
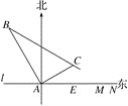
����Ŀ����ij�ɻ�����������ĵ���l����һ��Ϊ1 km�ķɻ��ܵ�MN(��ͼ)�����ܵ�MN��������14.5ǧ�״���һ�۲�վA.ijʱ�̲��һ������ֱ�߽���ķɻ�λ�ڵ�A�ı�ƫ��30���������A���15ǧ��B��������1���ӣ��ֲ�ø÷ɻ�λ�ڵ�A�ı�ƫ��60���������A���5![]() ǧ��C����
ǧ��C����
(1)�÷ɻ����е��ٶ��Ƕ���ǧ��/Сʱ��(�����������)
(2)����÷ɻ����ı亽��������У���ô�ɻ��ܷ������ܵ�MN֮�䣿��˵�����ɣ�
���𰸡�(1)�ɻ����е��ٶ�Ϊ600![]() km/h��(2)�ܽ������ܵ�MN֮�䣬���ɼ�����.
km/h��(2)�ܽ������ܵ�MN֮�䣬���ɼ�����.
��������
��1���������BAC=90�㣬Ȼ�����ù��ɶ�����ʽ��⼴�ɵõ�BC������⼴�ɣ�
��2����CE��l��E����ֱ��BC��l��F��Ȼ�����CE��AE��Ȼ�����AF�ij����ٽ����жϼ��ɣ�
�⣺(1)�����⣬�á�BAC��90����
��BC��![]() ��10
��10![]() ��
��
��ɻ����е��ٶ�Ϊ10![]() ��60��600
��60��600![]() (km/h).
(km/h).
(2)�ܽ������ܵ�MN֮�䣮
���ɣ���CE��l�ڵ�E����ֱ��BC��l�ڵ�F.
��Rt��ABC��AC��5![]() ��BC��10
��BC��10![]() ��
��
���ABC��30��������BCA��60����
�֡ߡ�CAE��30������ACE����FCE��60����
��CE��AC��sin ��CAE��![]() ��
��
AE��AC��cos ��CAE��![]() .
.
��AF��2AE��15(km)��
��AN��AM��MN��14.5��1��15.5 km��
��AM��AF��AN��
��ɻ����ı亽��������У����������ܵ�MN֮�䣮