题目内容
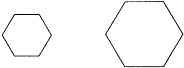
两个相似的六边形，如果一组对应边的长分别为3cm，4cm，且它们面积的差为28cm2，则较大的六边形的面积为
- A.44.8cm2
- B.45cm2
- C.64cm2
- D.54cm2
C
分析：根据相似三角形的面积比等于相似比的平方，设出两个相似六边形的面积，再根据二者面积的差为28cm2列出方程解答．
解答：∵两个六边形的一组对应边的长分别为3cm，4cm，
∴其面积比为32：42=9：16，
∴设两正六边形的面积分别为9x和16x，
根据题意列方程得，16x-9x=28，
即7x=28，
x=4．
则较大正六边形的面积为4×16=64cm2．
故选C．
点评：此题考查了“相似三角形的面积比等于相似比的平方”，根据一组对应边的长分别为3cm，4cm求出面积比是解题的关键．
分析：根据相似三角形的面积比等于相似比的平方，设出两个相似六边形的面积，再根据二者面积的差为28cm2列出方程解答．
解答：∵两个六边形的一组对应边的长分别为3cm，4cm，
∴其面积比为32：42=9：16，
∴设两正六边形的面积分别为9x和16x，
根据题意列方程得，16x-9x=28，
即7x=28，
x=4．
则较大正六边形的面积为4×16=64cm2．
故选C．
点评：此题考查了“相似三角形的面积比等于相似比的平方”，根据一组对应边的长分别为3cm，4cm求出面积比是解题的关键．
练习册系列答案
相关题目
27、我们约定，若一个三角形（记为△A1）是由另一个三角形（记为△A）通过一次平移，或绕其任一边的中点旋转180°得到的，则称△A1是由△A复制的．以下的操作中每一个三角形只可以复制一次，复制过程可以一直进行下去．如图1是由△A复制出△A1，又由△A1复制出△A2，再由△A2复制出△A3，形成了一个大三角形，记作△B．以下各题中的复制均是由△A开始的，由复制形成的多边形中的任意两个小三角形（指与△A全等的三角形）之间既无缝隙也无重叠．
