Question

【题目】某工厂将地处A,B两地的两个小工厂合成一个大厂,为了方便A,B两地职工的联系,企业准备在相距2km的A,B两地之间修一条笔直的公路(即图中的线段AB),经测量在A地的北偏东60°方向,B地的北偏西45°方向的C处有一以C点为中心,半径为0.7km的圆形公园,则修筑的这条公路会不会穿过公园?为什么?(提示:判断以点C为圆心的圆与AB的关系)

Answer 1

【答案】计划修筑的这条公路不会穿过公园

【解析】

要判断是否穿过公园，只需求得点C到AB的垂线段的长度，然后和半径进行比较即可．

过点C作CD⊥AB，垂足为D.

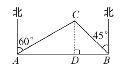
∵∠CBA=45°，

∴∠BCD=45°，

CD=BD，

设CD=x，则BD=x，由∠CAB=30°知AC=2x，

AD==x，

∴x+x=2，x=-1，

即CD=-1≈0.732(km)>0.7km，

也就是说，以C为圆心，以0.7km为半径的圆与AB相离.

所以计划修筑的这条公路不会穿过公园.