Question

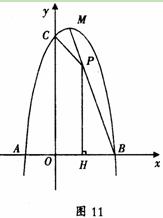
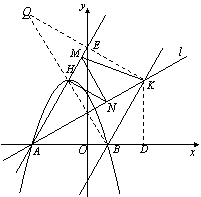
已知,如图11,二次函数图象的顶点为,与轴交于、两点(在点右侧),点、关于直线:对称.

(1)求、两点坐标,并证明点在直线上;

(2)求二次函数解析式;

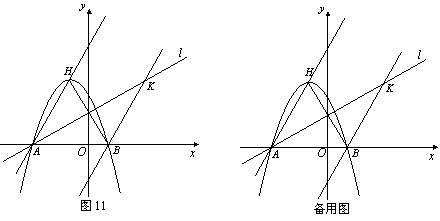
(3)过点作直线∥交直线于点,、分别为直线和直线上的两个动点,连接、、,求和的最小值.

 

Answer 1

解:(1)依题意,得

解得,

∵点在点右侧

∴点坐标为,点坐标为

∵直线:

当时,

∴点在直线上

(2)∵点、关于过点的直线:对称

            ∴

            过顶点作交于点

则,

            ∴顶点 

            代入二次函数解析式,解得

            ∴二次函数解析式为

(3)直线的解析式为

      直线的解析式为

            由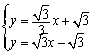 解得 即,则

            ∵点、关于直线对称

            ∴的最小值是,

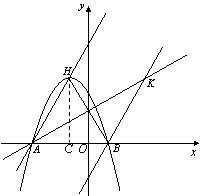
            过点作直线的对称点,连接,交直线于

则,,

            ∴的最小值是,即的长是的最小值

            ∵∥

            ∴

            由勾股定理得

            ∴的最小值为