Question

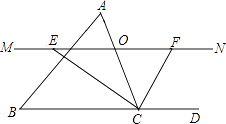
【题目】如图，长方形纸片ABCD，点E、F分别在边AB、CD上，连接EF，将∠BEF对折点B落在直线EF上的点B′处，得折痕EM；将∠AEF对折，点A落在直线EF上的点A′处，得折痕EN，求∠NEM的度数，并直接写出∠B′ME互余的角.

Answer 1

【答案】证明见解析

【解析】试题分析：由折叠的性质得到∠MB′E=∠B=90°，∠NA′E=∠A=90°，∠MEB=∠MEB′，∠AEN=∠A′EN，再由平角的定义得到∠NEM的度数，然后互为余角的性质求解即可.

试题解析：由翻折的性质可得：∠AEN=∠A′EN，∠BEM=∠B′EM

∠NEM=∠A′EN+∠B′EM=∠AEA′+∠B′EB=×180°=90°

由翻折性质可知：∠MB′E=∠B=90°

由直角三角形两锐角互余可知：∠B′ME的一个余角是∠B′EM

∠BEM=∠B′EM ∠BEM也是∠B′ME的一个余角

∠NEF+∠B′EM=90° ∠NEF=∠B′ME

∠ANE，∠A′NE也是∠B′ME的余角