题目内容
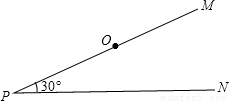
如图,PM,PN是两条夹角为30°的笔直的公路,在距离点P为8千米的点O处,有一个小灵通信号发射中心,在它的周围5千米(包括5千米)范围内小灵通才可以正常使用.小王早上8:00钟从点P出发,乘坐速度为每小时30千米的汽车向PN方向行进,若小王身上带的通讯工具只有小灵通,现要打电话给小王,问在什么时刻开始拨打为好?通话时间最多可以是几分钟?(结果精确到分)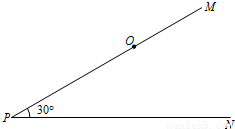
【答案】分析:首先过O作OD垂直PN,交PN于D.直接根据直角三角形中的三角函数求解可得OD=8×sin30°=4;以点O为圆心,5为半径作圆,与PN相交于点E,F.则DE=3,即可求出EF的长以及PE的长,进而求出通话时间.
解答: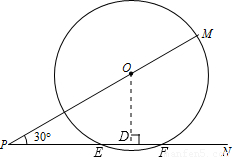 解:过O作OD垂直PN,交PN于D.以点O为圆心,5为半径作圆,与PN相交于点E,F.
解:过O作OD垂直PN,交PN于D.以点O为圆心,5为半径作圆,与PN相交于点E,F.
OD=8×sin30°=4km,
∵OD=4km,OE=5km,
∴DE=3km,EF=6km,
∵PD=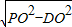 =
=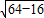 =4
=4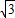 ≈6.8km,
≈6.8km,
PE=PD-DE=3.8km.
3.8÷30×60≈8分钟,
所以到8:08打电话,则通话时间为:EF÷30=6÷30=0.2(小时),
∴0.2×60=12分钟,
答:在8:08时刻开始拨打为好,通话时间最多可以是12分钟.
点评:此题主要考查了直线和圆的位置关系以及解直角三角形,解此类问题一般要把半径、弦心距、弦的一半构建在一个直角三角形里,运用勾股定理求解.
解答:
 解:过O作OD垂直PN,交PN于D.以点O为圆心,5为半径作圆,与PN相交于点E,F.
解:过O作OD垂直PN,交PN于D.以点O为圆心,5为半径作圆,与PN相交于点E,F. OD=8×sin30°=4km,
∵OD=4km,OE=5km,
∴DE=3km,EF=6km,
∵PD=
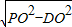 =
=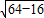 =4
=4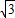 ≈6.8km,
≈6.8km,PE=PD-DE=3.8km.
3.8÷30×60≈8分钟,
所以到8:08打电话,则通话时间为:EF÷30=6÷30=0.2(小时),
∴0.2×60=12分钟,
答:在8:08时刻开始拨打为好,通话时间最多可以是12分钟.
点评:此题主要考查了直线和圆的位置关系以及解直角三角形,解此类问题一般要把半径、弦心距、弦的一半构建在一个直角三角形里,运用勾股定理求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
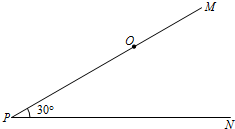 如图,PM,PN是两条夹角为30°的笔直的公路,在距离点P为8千米的点O处,有一个小灵通信号发射中心,在它的周围5千米(包括5千米)范围内小灵通才可以正常使用.小王早上8:00钟从点P出发,乘坐速度为每小时30千米的汽车向PN方向行进,若小王身上带的通讯工具只有小灵通,现要打电话给小王,问在什么时刻开始拨打为好?通话时间最多可以是几分钟?(结果精确到分)
如图,PM,PN是两条夹角为30°的笔直的公路,在距离点P为8千米的点O处,有一个小灵通信号发射中心,在它的周围5千米(包括5千米)范围内小灵通才可以正常使用.小王早上8:00钟从点P出发,乘坐速度为每小时30千米的汽车向PN方向行进,若小王身上带的通讯工具只有小灵通,现要打电话给小王,问在什么时刻开始拨打为好?通话时间最多可以是几分钟?(结果精确到分)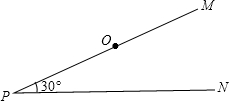 如图,PM,PN是两条夹角为30°的笔直的公路,在距离点P为8千米的点O处,有一个小灵通信号发射中心,在它的周围5千米(包括5千米)范围内小灵通才可以正常使用.小王早上8:00钟从点P出发,乘坐速度为每小时30千米的汽车向PN方向行进.
如图,PM,PN是两条夹角为30°的笔直的公路,在距离点P为8千米的点O处,有一个小灵通信号发射中心,在它的周围5千米(包括5千米)范围内小灵通才可以正常使用.小王早上8:00钟从点P出发,乘坐速度为每小时30千米的汽车向PN方向行进.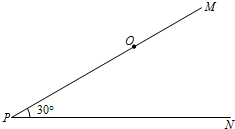 如图,PM,PN是两条夹角为30°的笔直的公路,在距离点P为8千米的点O处,有一个小灵通信号发射中心,在它的周围5千米(包括5千米)范围内小灵通才可以正常使用.小王早上8:00钟从点P出发,乘坐速度为每小时30千米的汽车向PN方向行进,若小王身上带的通讯工具只有小灵通,现要打电话给小王,问在什么时刻开始拨打为好?通话时间最多可以是几分钟?(结果精确到分)
如图,PM,PN是两条夹角为30°的笔直的公路,在距离点P为8千米的点O处,有一个小灵通信号发射中心,在它的周围5千米(包括5千米)范围内小灵通才可以正常使用.小王早上8:00钟从点P出发,乘坐速度为每小时30千米的汽车向PN方向行进,若小王身上带的通讯工具只有小灵通,现要打电话给小王,问在什么时刻开始拨打为好?通话时间最多可以是几分钟?(结果精确到分)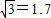 )
)