题目内容
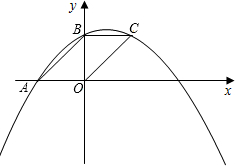
已知抛物线y=-x2-(m-4)x+3(m-1)与x轴交于A、B两点,与y轴交于C点.(1)求m的取值范围;
(2)若m≤0,直线y=kx-1,经过点A,与y轴交于点D,且AD×BD=2
| 5 |
(3)若点A在点B的左边,在第一象限内,(2)中所得抛物线上是否存在一点P,使直线PA平分△ACD的面积?若存在,求出P点坐标,若不存在,请说明理由.
分析:(1)由于抛物线与x轴有两个不同的交点,可令y=0,则所得方程的根的判别式△>0,可据此求出m的取值范围.
(2)根据已知直线的解析式,可得到D点的坐标;根据抛物线的解析式,可用m表示出A、B的坐标,即可得到AD、BD的长,代入AD×BD=2
中,即可求得m的值,从而确定抛物线的解析式.
(3)根据(2)题所得抛物线即可确定A、B、C的坐标;假设存在符合条件的P点,设直线PA与y轴的交点为E,若PA将△ACD分成面积相等的两部分,那么DE=CE,由此可求出E点的坐标,进而可求出直线AE(即PA)的解析式,联立抛物线的解析式即可求得P点坐标.(若直线与抛物线只有一个交点,就说明不存在符合条件的P点.)
(2)根据已知直线的解析式,可得到D点的坐标;根据抛物线的解析式,可用m表示出A、B的坐标,即可得到AD、BD的长,代入AD×BD=2
| 5 |
(3)根据(2)题所得抛物线即可确定A、B、C的坐标;假设存在符合条件的P点,设直线PA与y轴的交点为E,若PA将△ACD分成面积相等的两部分,那么DE=CE,由此可求出E点的坐标,进而可求出直线AE(即PA)的解析式,联立抛物线的解析式即可求得P点坐标.(若直线与抛物线只有一个交点,就说明不存在符合条件的P点.)
解答:解:(1)∵抛物线与x轴有两个不同的交点,
∴△=(m-4)2+12(m-1)=m2+4m+4=(m+2)2>0,
∴m≠-2.
(2)∵y=-x2-(m-4)x+3(m-1)=-(x-3)(x+m-1),
∴抛物线与x轴的两个交点为:(3,0),(1-m,0);
易知D(0,-1),则有:
AD×BD=
×
=2
,
∴10×(m2-2m+2)=20,
即m2-2m=0,
解得m=0,m=2(舍去),
∴抛物线的解析式为:y=-x2+4x-3.
(3)若点A在点B左侧,则:A(1,0),B(3,0),C(0,-3);
假设存在符合题意的P点,设直线PA与y轴的交点为E,
若AE平分△DAC的面积,
则有:DE=CE,即E(0,-2);
∴直线AE的解析式为:y=2x-2;
联立抛物线的解析式有
,
解得
;
即直线AE与抛物线只有一个交点A,因此不存在符合条件的P点.
∴△=(m-4)2+12(m-1)=m2+4m+4=(m+2)2>0,
∴m≠-2.
(2)∵y=-x2-(m-4)x+3(m-1)=-(x-3)(x+m-1),
∴抛物线与x轴的两个交点为:(3,0),(1-m,0);
易知D(0,-1),则有:
AD×BD=
| 32+12 |
| (1-m)2+12 |
| 5 |
∴10×(m2-2m+2)=20,
即m2-2m=0,
解得m=0,m=2(舍去),
∴抛物线的解析式为:y=-x2+4x-3.
(3)若点A在点B左侧,则:A(1,0),B(3,0),C(0,-3);
假设存在符合题意的P点,设直线PA与y轴的交点为E,
若AE平分△DAC的面积,
则有:DE=CE,即E(0,-2);
∴直线AE的解析式为:y=2x-2;
联立抛物线的解析式有
|
解得
|
即直线AE与抛物线只有一个交点A,因此不存在符合条件的P点.
点评:此题考查了根的判别式、二次函数解析式的确定、勾股定理、函数图象的交点坐标及图形面积的求法,难度适中.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
| A、4 | B、8 | C、-4 | D、16 |
 (1)求b+c的值;
(1)求b+c的值;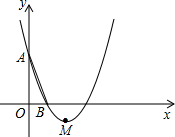 (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.