��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y= x+1�ֱ����������ύ��B��A���㣬CΪ��ֱ���ϵ�һ���㣬��ÿ��1����λ���ȵ��ٶȴӵ�A��ʼ��ֱ��BA�����ƶ������ȱߡ�CDE����D�͵�E����x���ϣ��Ե�CΪ�����������y=a��x��m��2+n������E����M��x�ᡢֱ��AB�����У���뾶Ϊ3��1��
x+1�ֱ����������ύ��B��A���㣬CΪ��ֱ���ϵ�һ���㣬��ÿ��1����λ���ȵ��ٶȴӵ�A��ʼ��ֱ��BA�����ƶ������ȱߡ�CDE����D�͵�E����x���ϣ��Ե�CΪ�����������y=a��x��m��2+n������E����M��x�ᡢֱ��AB�����У���뾶Ϊ3��1�� ��a��
��a��

��1�����A������͡�ABO�Ķ�����
��2������C���A�غ�ʱ����a��ֵ��
��3����C�ƶ�������ʱ���ȱߡ�CDE�ı�CE��һ�����M���У�
 x+1�ֱ����������ύ��B��A���㣬CΪ��ֱ���ϵ�һ���㣬��ÿ��1����λ���ȵ��ٶȴӵ�A��ʼ��ֱ��BA�����ƶ������ȱߡ�CDE����D�͵�E����x���ϣ��Ե�CΪ�����������y=a��x��m��2+n������E����M��x�ᡢֱ��AB�����У���뾶Ϊ3��1��
x+1�ֱ����������ύ��B��A���㣬CΪ��ֱ���ϵ�һ���㣬��ÿ��1����λ���ȵ��ٶȴӵ�A��ʼ��ֱ��BA�����ƶ������ȱߡ�CDE����D�͵�E����x���ϣ��Ե�CΪ�����������y=a��x��m��2+n������E����M��x�ᡢֱ��AB�����У���뾶Ϊ3��1�� ��a��
��a��
��1�����A������͡�ABO�Ķ�����
��2������C���A�غ�ʱ����a��ֵ��
��3����C�ƶ�������ʱ���ȱߡ�CDE�ı�CE��һ�����M���У�
��1��A�������ǣ�0��1������ABO=30�㣻��2����3����3��4��
�����������1����ֱ֪��AB�Ľ���ʽ�������ʽ��x=0���ܵõ�A�����ꣻ��y=0���ܵõ�B�����ꣻ��Rt��OAB�У�֪��OA��OB�ij��������к������ɵõ���ABO�Ķ�����
��2����C��A�غ�ʱ�������˵�C�����꣬Ȼ����OC�ij��Լ��ȱ������ε��������OD��OE�ij������ɵõ�D��E�����꣬���ô���ϵ������ȷ��a��ֵ��
��3��������Ҫ���ͼ�����⣬���Ȼ�����һ������ʱ��ʾ��ͼ��������ͼ������֪������ֻ��Բ�İ뾶����ô������Բ���������е��Լ���E���������жϳ��ı���CPMN�������Σ���ôCP���M�İ뾶��ȣ�ֻҪ�����PE���ܽ�һ�����C�����ꣻ��ô���Դ�PE=EQ����Rt��MEP���֣����ȡ�CED=60�㣬����MEP=��MEQ��������������ǵĶ�����ͨ����ֱ�������β��ѵõ�PE�ij����������PE����C��E�����꣮Ȼ������C��E������ȷ��a��ֵ�����������AC�ij����ɴ˵ý⣮
��1����x=0ʱ��y=1����y=0ʱ��x=-
 ��
����OA=1��OB=
 ��
��
��A�������ǣ�0��1��
��ABO=30�㣮
��2���ߡ�CDEΪ�ȱߡ�����A��0��1����

��D�������ǣ�
 ��0����E�������ǣ�
��0����E�������ǣ� ��0����
��0�����ѵ�A��0��1����D��
 ��0����E��
��0����E�� ��0�������� y=a��x-m��2+n��
��0�������� y=a��x-m��2+n����ã�a=-3��
��3����ͼ�����е�ֱ���Q��N��P������MQ��MN��MP��ME������C��CH��x�ᣬHΪ���㣬��A��AF��CH��FΪ���㣮

�ߡ�CDE�ǵȱ������Σ���ABO=30��
���BCE=90�㣬��ECN=90��
��CE��AB�ֱ����M���У����MPC=��CNM=90�㣬���ı���MPCNΪ���Σ���MP=MN
���ı���MPCNΪ������
��MP=MN=CP=CN=3��1-
 ��a��a��0����
��a��a��0������EC��x�ᶼ���M���У���EP=EQ��
�ߡ�NBQ+��NMQ=180�㣬���PMQ=60��
���EMQ=30�㣬����Rt��MEP�У�tan30��=
 ����PE=��
����PE=�� -3��a
-3��a��CE=CP+PE=3��1-
 ��a+��
��a+�� -3��a=-2
-3��a=-2 a
a��DH=HE=-
 a��CH=-3a��BH=-3
a��CH=-3a��BH=-3 a��
a����OH=-3
 a-
a- ��OE=-4
��OE=-4 a-
a-
��E��-4
 a-
a- ��0��
��0����C��-3
 a-
a- ��-3a��
��-3a������κ����Ľ���ʽΪ��y=a��x+3
 a+
a+ ��2-3a
��2-3a��E�ڸ���������
��a��-4
 a-
a- +3
+3 a+
a+ ��2-3a=0
��2-3a=0�ã�a2=1����֮��a1=1��a2=-1
��a��0����a=-1
��AF=2
 ��CF=2����AC=4
��CF=2����AC=4���C�ƶ���4��ʱ���ȱߡ�CDE�ı�CE��һ�����M���У�
�����������Ѷ������漰���������⣬������ֵ�����Ǿ���ֵ����3�����У���ȷ������ͼ���᳹���ν�ϵĽ���˼���ǹؼ���

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 ��x��0����ͼ���ཻ��A�㣬��y�ᡢx��ֱ��ཻ��B��C���㣬��C��2��0����A��ĺ�����Ϊ-1.
��x��0����ͼ���ཻ��A�㣬��y�ᡢx��ֱ��ཻ��B��C���㣬��C��2��0����A��ĺ�����Ϊ-1.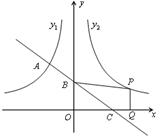
 ��x��0����ͼ����
��x��0����ͼ���� ��x��0����ͼ�����y��Գƣ���
��x��0����ͼ�����y��Գƣ���
 �ֱ��ʾ�ڹ���������е�·�̣�tΪʱ�䣬������ͼ������������Ǻϵ��ǣ� ��
�ֱ��ʾ�ڹ���������е�·�̣�tΪʱ�䣬������ͼ������������Ǻϵ��ǣ� ��
 �뺯��
�뺯�� ��ͬһ����ϵ�еĴ���ͼ������ͼ�е� �� ��
��ͬһ����ϵ�еĴ���ͼ������ͼ�е� �� ��
 ������ʵ��k����0��k��1��
������ʵ��k����0��k��1��