题目内容
【题目】(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=![]() ∠BAD.求证:EF=BE+FD;
∠BAD.求证:EF=BE+FD;
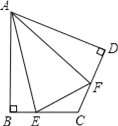
(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=![]() ∠BAD,(1)中的结论是否仍然成立?
∠BAD,(1)中的结论是否仍然成立?
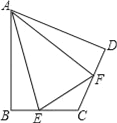
(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=![]() ∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
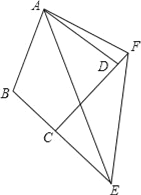
【答案】(1)证明见解析;(2)(2)(1)中的结论EF=BE+FD仍然成立;(3)结论EF=BE+FD不成立,应当是EF=BE﹣FD,证明见解析.
【解析】试题分析:(1)可通过构建全等三角形来实现线段间的转换.延长EB到G,使BG=DF,连接AG.目的就是要证明三角形AGE和三角形AEF全等将EF转换成GE,那么这样EF=BE+DF了,于是证明两组三角形全等就是解题的关键.三角形ABE和AEF中,只有一条公共边AE,我们就要通过其他的全等三角形来实现,在三角形ABG和AFD中,已知了一组直角,BG=DF,AB=AD,因此两三角形全等,那么AG=AF,∠1=∠2,那么∠1+∠3=∠2+∠3=∠EAF=![]() ∠BAD.由此就构成了三角形ABE和AEF全等的所有条件(SAS),那么就能得出EF=GE了.
∠BAD.由此就构成了三角形ABE和AEF全等的所有条件(SAS),那么就能得出EF=GE了.
(2)思路和作辅助线的方法与(1)完全一样,只不过证明三角形ABG和ADF全等中,证明∠ABG=∠ADF时,用到的等角的补角相等,其他的都一样.因此与(1)的结果完全一样.
(3)按照(1)的思路,我们应该通过全等三角形来实现相等线段的转换.就应该在BE上截取BG,使BG=DF,连接AG.根据(1)的证法,我们可得出DF=BG,GE=EF,那么EF=GE=BE-BG=BE-DF.所以(1)的结论在(3)的条件下是不成立的.
(1)延长EB到G,使BG=DF,连接AG.
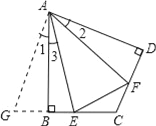
∵∠ABG=∠ABC=∠D=90°,AB=AD,
∴△ABG≌△ADF.
∴AG=AF,∠1=∠2.
∴∠1+∠3=∠2+∠3=∠EAF=![]() ∠BAD.
∠BAD.
∴∠GAE=∠EAF.
又AE=AE,
∴△AEG≌△AEF.
∴EG=EF.
∵EG=BE+BG.
∴EF=BE+FD
(2)(1)中的结论EF=BE+FD仍然成立.
(3)结论EF=BE+FD不成立,应当是EF=BE﹣FD.
证明:在BE上截取BG,使BG=DF,连接AG.
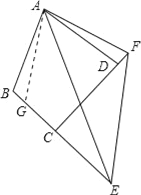
∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,
∴∠B=∠ADF.
∵AB=AD,
∴△ABG≌△ADF.
∴∠BAG=∠DAF,AG=AF.
∴∠BAG+∠EAD=∠DAF+∠EAD
=∠EAF=![]() ∠BAD.
∠BAD.
∴∠GAE=∠EAF.
∵AE=AE,
∴△AEG≌△AEF.
∴EG=EF
∵EG=BE﹣BG
∴EF=BE﹣FD.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案