题目内容
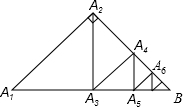 如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,…以此类推,则线段A2nA2n+1(n为正整数)的长为
如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,…以此类推,则线段A2nA2n+1(n为正整数)的长为
| ||
| 2n-2 |
| ||
| 2n-2 |
分析:根据等腰直角三角形的直角边与斜边的关系求出A2A3,再根据等腰直角三角形斜边上的高线平分斜边可得A4A5=
A2A3,以此类推,后一条线段是前一条线段的
,然后写出线段A2nA2n+1即可得解.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵∠A1A2B=90°,A1A2=A2B=4,A2A3⊥A1B,
∴A2A3=
A1A2=
×4=2
,
∵A3A4⊥A2B,A4A5⊥A3B,
∴A4为A2B的中点,A5为A3B的中点,
∴A4A5=
A2A3=
×2
=
,即A2×2A2×2+1=
,
…,
以此类推,A6A7=
A4A5=
,即A2×3A2×3+1=
,
…,
A2nA2n+1=
.
故答案为:
.
∴A2A3=
| ||
| 2 |
| ||
| 2 |
| 2 |
∵A3A4⊥A2B,A4A5⊥A3B,
∴A4为A2B的中点,A5为A3B的中点,
∴A4A5=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
…,
以此类推,A6A7=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
…,
A2nA2n+1=
| ||
| 2n-2 |
故答案为:
| ||
| 2n-2 |
点评:本题考查了等腰直角三角形的性质,主要利用了等腰直角三角形直角边是斜边的
,等腰直角三角形斜边上的高线也是斜边的中线,三角形的三角形的中位线平行于第三边并且等于第三边的一半.
| ||
| 2 |

练习册系列答案
相关题目
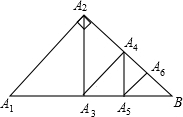 如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,则线段A5A6的长为
如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,则线段A5A6的长为 如图,△A1A2B是等腰直角三角形,∠A1A2B=90°,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,…,An+1An+2⊥AnB,垂足为An+2(n为正整数),若A1A2=A2B=a,则线段An+1An+2的长为( )
如图,△A1A2B是等腰直角三角形,∠A1A2B=90°,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,…,An+1An+2⊥AnB,垂足为An+2(n为正整数),若A1A2=A2B=a,则线段An+1An+2的长为( ) 如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,一直按此做下去,…则△AnAn+1B的面积为
如图,△A1A2B是直角三角形,∠A1A2B=90°,且A1A2=A2B=4,A2A3⊥A1B,垂足为A3,A3A4⊥A2B,垂足为A4,A4A5⊥A3B,垂足为A5,A5A6⊥A4B,垂足为A6,一直按此做下去,…则△AnAn+1B的面积为 )n
)n