题目内容
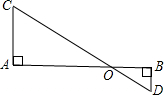 如图,已知AC⊥AB,BD⊥AB,AO=78cm,BO=42cm,CD=159cm,求CO和DO.
如图,已知AC⊥AB,BD⊥AB,AO=78cm,BO=42cm,CD=159cm,求CO和DO.
分析:根据题意,易证△AOC∽△BDO,根据相似三角形的判定与性质,列出比例等式即可解得CO和DO的长.
解答:解:设DO=xcm,则CO=(159-x)cm,
∵AC⊥AB,BD⊥AB,∠A=∠B=90°,∠AOC=∠BOD,
∴△AOC∽△BDO.
∴
=
.
即
=
.
∴x=55.65.
∴CO=103.35cm,DO=55.65cm.
∵AC⊥AB,BD⊥AB,∠A=∠B=90°,∠AOC=∠BOD,
∴△AOC∽△BDO.
∴
| AO |
| BO |
| CO |
| DO |
即
| 78 |
| 42 |
| 159-x |
| x |
∴x=55.65.
∴CO=103.35cm,DO=55.65cm.
点评:此题考查了相似三角形的判定和性质:
①有两个对应角相等的三角形相似;
②有两个对应边的比相等,且其夹角相等,则两个三角形相似;
③三组对应边的比相等,则两个三角形相似;
性质:相似三角形的对应角相等,对应边的比相等.
①有两个对应角相等的三角形相似;
②有两个对应边的比相等,且其夹角相等,则两个三角形相似;
③三组对应边的比相等,则两个三角形相似;
性质:相似三角形的对应角相等,对应边的比相等.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 28、如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论.
28、如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论. 21、如图,已知AC=AB、AE=AD,∠EAB=∠DAC,求证:BD=CE.
21、如图,已知AC=AB、AE=AD,∠EAB=∠DAC,求证:BD=CE. 如图,已知AC=AB,AE=AD,∠EAB=∠DAC,问BD与EC相等吗?说明理由.
如图,已知AC=AB,AE=AD,∠EAB=∠DAC,问BD与EC相等吗?说明理由.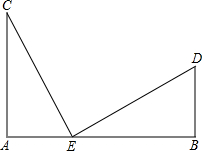 如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD.
如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD.