题目内容
学完分式运算后,老师出了一道题“化简:
+
”.
小明的做法是:原式=
-
=
=
;
小亮的做法是:原式=(x+3)(x-2)+(2-x)=x2+x-6+2-x=x2-4;
小芳的做法是:原式=
-
=
-
=
=1.
其中正确的是( )
| x+3 |
| x+2 |
| 2-x |
| x2-4 |
小明的做法是:原式=
| (x+3)(x-2) |
| x2-4 |
| x-2 |
| x2-4 |
| x2+x-6-x-2 |
| x2-4 |
| x2-8 |
| x2-4 |
小亮的做法是:原式=(x+3)(x-2)+(2-x)=x2+x-6+2-x=x2-4;
小芳的做法是:原式=
| x+3 |
| x+2 |
| x-2 |
| (x+2)(x-2) |
| x+3 |
| x+2 |
| 1 |
| x+2 |
| x+3-1 |
| x+2 |
其中正确的是( )
| A、小明 | B、小亮 |
| C、小芳 | D、没有正确的 |
分析:小明的做法在通分后分子(x-2)的符号没有变换;
小亮的做法把分母忘记写了;
小芳的做法是正确的.
小亮的做法把分母忘记写了;
小芳的做法是正确的.
解答:解:
+
=
-
=
-
=
=
=1.
所以正确的应是小芳.
故选C.
| x+3 |
| x+2 |
| 2-x |
| x2-4 |
=
| x+3 |
| x+2 |
| x-2 |
| (x+2)(x-2) |
=
| x+3 |
| x+2 |
| 1 |
| x+2 |
=
| x+3-1 |
| x+2 |
=
| x+2 |
| x+2 |
=1.
所以正确的应是小芳.
故选C.
点评:本题考查了分式的计算和化简.解决这类题目关键是把握好通分与约分.分式加减的本质是通分,乘除的本质是约分.同时注意在进行运算前要尽量保证每个分式最简.化简
=-
时,学生容易出错.同时学生也容易混淆计算与解方程的区别,而误选B.
| 2-x |
| x2-4 |
| 1 |
| x+2 |

练习册系列答案
相关题目
 ”
”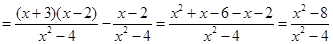 ;
; ;
;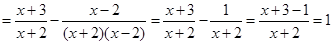 .
. ”.
”. ;
; .
.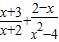 ”.
”. ;
; .
.