题目内容
如图,正比例函数 的图象与反比例函数
的图象与反比例函数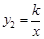 (
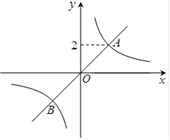
( )的图象相交于A、B两点,点A的纵坐标为2.(1)求反比例函数的解析式;(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量
)的图象相交于A、B两点,点A的纵坐标为2.(1)求反比例函数的解析式;(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量 的取值范围.
的取值范围.
 的图象与反比例函数
的图象与反比例函数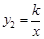 (
( )的图象相交于A、B两点,点A的纵坐标为2.(1)求反比例函数的解析式;(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量
)的图象相交于A、B两点,点A的纵坐标为2.(1)求反比例函数的解析式;(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量 的取值范围.
的取值范围.
(1)反比例函数的解析式为: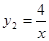 ;(2)B(-2,-2),自变量的取值范围是:-2<x<0或x>2.
;(2)B(-2,-2),自变量的取值范围是:-2<x<0或x>2.
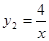 ;(2)B(-2,-2),自变量的取值范围是:-2<x<0或x>2.
;(2)B(-2,-2),自变量的取值范围是:-2<x<0或x>2.试题分析:(1)由于点A的纵坐标已知,正比例函数已知,且点A在正比例函数上,所以将点A的纵坐标代入正比例函数的解析式中,即可求出点A的横坐标,然后将点A的横纵坐标代入反比例函数解析式中,即可求出k的值,从而求出反比例函数的解析式.(2)由于点B是正比例函数与反比例函数的图象的交点,所以有y1=y2,从而求得点B的坐标.y1>y2,从图象上看,就是直线在双曲线的上方,利用图象即可求出范围.
试题解析:(1)设A点的坐标为(m,2),代入
 得:
得: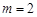 ,所以点A的坐标为(2,2).∴
,所以点A的坐标为(2,2).∴ .
.∴反比例函数的解析式为:
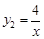 .(3分)
.(3分)(2)当
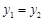 时,
时,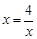 .解得
.解得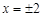 .∴点B的坐标为(-2,- 2).
.∴点B的坐标为(-2,- 2).或者由反比例函数、正比例函数图象的对称性得点B的坐标为(-2,- 2).
由图象可知,当
 时,自变量
时,自变量 的取值范围是:
的取值范围是: 或
或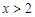 .
. 
练习册系列答案
相关题目
 的图像与反比例函数
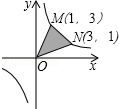
的图像与反比例函数 的图象交于A(-2,1),B(1,n)两点.
的图象交于A(-2,1),B(1,n)两点.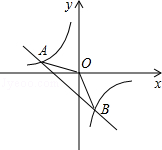
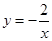 的图象在( )
的图象在( ) 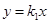 的图象于反比例函数
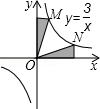
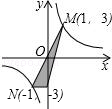
的图象于反比例函数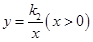 的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式.
的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式.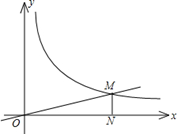
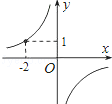
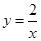
 1),(-3,
1),(-3, (k<0)的图像上,则
(k<0)的图像上,则