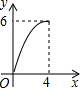题目内容
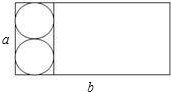 如图,矩形的长与宽分别为a和b,在矩形中截取两个大小相同的圆作为圆柱的上下底面,剩余的矩形作为圆柱的侧面,刚好能组合成一个没有空隙的圆柱,则a和b要满足什么数量关系
如图,矩形的长与宽分别为a和b,在矩形中截取两个大小相同的圆作为圆柱的上下底面,剩余的矩形作为圆柱的侧面,刚好能组合成一个没有空隙的圆柱,则a和b要满足什么数量关系
- A.
 =
=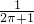
- B.
 =
=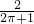
- C.
 =
=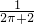
- D.
 =
=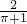
D
分析:利用圆柱的底面周长和剩余长方形的长之间的等量关系列出方程计算.
解答:组成圆柱后,圆柱的底面周长=剩余长方形的长.
 π=b-
π=b- ,即a(π+1)=2b,
,即a(π+1)=2b,
整理得 =
=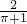 .
.
故选D.
点评:解决本题的关键是得到圆柱的底面周长和剩余长方形的长之间的等量关系.
分析:利用圆柱的底面周长和剩余长方形的长之间的等量关系列出方程计算.
解答:组成圆柱后,圆柱的底面周长=剩余长方形的长.
 π=b-
π=b- ,即a(π+1)=2b,
,即a(π+1)=2b,整理得
 =
=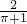 .
.故选D.
点评:解决本题的关键是得到圆柱的底面周长和剩余长方形的长之间的等量关系.

练习册系列答案
相关题目
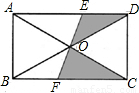
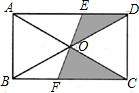 如图,矩形ABCD的对角线相交于点O,过点O的直线分别交AD、BC于点E、F,若矩形的长与宽分别是4cm、3cm,则阴影部分的面积是
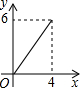
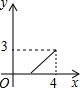
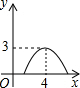
如图,矩形ABCD的对角线相交于点O,过点O的直线分别交AD、BC于点E、F,若矩形的长与宽分别是4cm、3cm,则阴影部分的面积是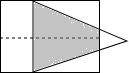 (2013•西宁)如图,矩形的长和宽分别是4和3,等腰三角形的底和高分别是3和4,如果此三角形的底和矩形的宽重合,并且沿矩形两条宽的中点所在的直线自右向左匀速运动至等腰三角形的底与另一宽重合.设矩形与等腰三角形重叠部分(阴影部分)的面积为y,重叠部分图形的高为x,那么y关于x的函数图象大致应为( )
(2013•西宁)如图,矩形的长和宽分别是4和3,等腰三角形的底和高分别是3和4,如果此三角形的底和矩形的宽重合,并且沿矩形两条宽的中点所在的直线自右向左匀速运动至等腰三角形的底与另一宽重合.设矩形与等腰三角形重叠部分(阴影部分)的面积为y,重叠部分图形的高为x,那么y关于x的函数图象大致应为( )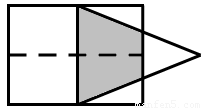
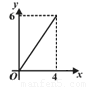 B.
B.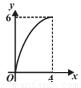 C.
C.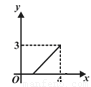 D.
D.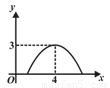
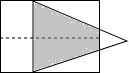 如图,矩形的长和宽分别是4和3,等腰三角形的底和高分别是3和4,如果此三角形的底和矩形的宽重合,并且沿矩形两条宽的中点所在的直线自右向左匀速运动至等腰三角形的底与另一宽重合.设矩形与等腰三角形重叠部分(阴影部分)的面积为y,重叠部分图形的高为x,那么y关于x的函数图象大致应为
如图,矩形的长和宽分别是4和3,等腰三角形的底和高分别是3和4,如果此三角形的底和矩形的宽重合,并且沿矩形两条宽的中点所在的直线自右向左匀速运动至等腰三角形的底与另一宽重合.设矩形与等腰三角形重叠部分(阴影部分)的面积为y,重叠部分图形的高为x,那么y关于x的函数图象大致应为