题目内容
 如图1,正方形每条边上放置相同数目的小球,设一条边上的小球数为n,请用含n的代数式表示正方形边上的所有小球数________;将正方形改为立方体,如图2,每条边上同样放置相同数目的小球,设一条边上的小球数仍为n,请用含n的代数式表示立方体上的所有小球数________.
如图1,正方形每条边上放置相同数目的小球,设一条边上的小球数为n,请用含n的代数式表示正方形边上的所有小球数________;将正方形改为立方体,如图2,每条边上同样放置相同数目的小球,设一条边上的小球数仍为n,请用含n的代数式表示立方体上的所有小球数________.
4n-4 12n-16
分析:正方形有4条边,每边上的小球数为n,则有4n个小球,而每个顶点处的小球重复计算一次,则正方形边上的所有小球的个数为4n-4;正方体有12条棱,每条棱上的小球数为n,则有12n个小球,而每个顶点处的小球重复计算2次,则正方形边上的所有小球的个数为12n-8×2.
解答:当一条边上的小球数为n,正方形边上的所有小球的个数为4n-4;
当一条边上的小球数为n,立方体上的所有小球数为12n-8×2=12n-16.
故答案为4n-4;12n-16.
点评:本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.
分析:正方形有4条边,每边上的小球数为n,则有4n个小球,而每个顶点处的小球重复计算一次,则正方形边上的所有小球的个数为4n-4;正方体有12条棱,每条棱上的小球数为n,则有12n个小球,而每个顶点处的小球重复计算2次,则正方形边上的所有小球的个数为12n-8×2.
解答:当一条边上的小球数为n,正方形边上的所有小球的个数为4n-4;
当一条边上的小球数为n,立方体上的所有小球数为12n-8×2=12n-16.
故答案为4n-4;12n-16.
点评:本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
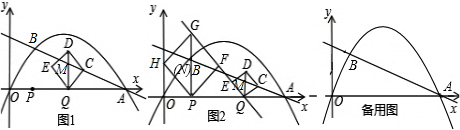

 (3)过点P作x轴的垂线,交抛物线于点N,延长PN到点G,使NG=PN,以PG为对角线作正方形P
(3)过点P作x轴的垂线,交抛物线于点N,延长PN到点G,使NG=PN,以PG为对角线作正方形P FGH(正方形PFGH随点P运动),当点P运动到点(2,0)时,如图2,正方形PFGH的边GP和正方形QCDE的边EQ落在同一条直线上.
FGH(正方形PFGH随点P运动),当点P运动到点(2,0)时,如图2,正方形PFGH的边GP和正方形QCDE的边EQ落在同一条直线上.
