题目内容
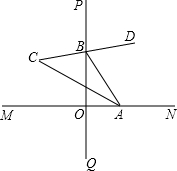
 小明用下面的方法画出了45°角:作两条互相垂直的直线MN、PQ,点A、B分别是MN、PQ上任意一点,作∠ABP的平分线BD,BD的反向延长线交∠OAB的平分线于点C,则∠C就是所求的45°角.你认为对吗?请给出证明.
小明用下面的方法画出了45°角:作两条互相垂直的直线MN、PQ,点A、B分别是MN、PQ上任意一点,作∠ABP的平分线BD,BD的反向延长线交∠OAB的平分线于点C,则∠C就是所求的45°角.你认为对吗?请给出证明.
解:正确.
理由如下:根据三角形的外角性质,∠ABD=∠C+∠BAC,∠ABP=∠BAO+∠AOB,
∵BD是∠ABP的平分线,AC是∠OAB的平分线,
∴∠ABD= ∠ABP,∠BAC=
∠ABP,∠BAC= ∠BAO,
∠BAO,
∴∠C+∠BAC= (∠BAO+∠AOB)=
(∠BAO+∠AOB)= ∠BAO+
∠BAO+ ∠AOB=∠BAC+
∠AOB=∠BAC+ ∠AOB,
∠AOB,
∴∠C= ∠AOB,
∠AOB,
∵∠AOB=90°,
∴∠C=45°.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式表示出∠ABD、∠ABP,再根据角平分线的定义可得∠ABD= ∠ABP,∠BAC=
∠ABP,∠BAC= ∠BAO,然后整理即可得到∠C=
∠BAO,然后整理即可得到∠C= ∠AOB,从而得解.
∠AOB,从而得解.
点评:本题考查了 三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,准确识图,找出各角度的关系是解题的关键.
理由如下:根据三角形的外角性质,∠ABD=∠C+∠BAC,∠ABP=∠BAO+∠AOB,
∵BD是∠ABP的平分线,AC是∠OAB的平分线,
∴∠ABD=
 ∠ABP,∠BAC=
∠ABP,∠BAC= ∠BAO,
∠BAO,∴∠C+∠BAC=
 (∠BAO+∠AOB)=
(∠BAO+∠AOB)= ∠BAO+
∠BAO+ ∠AOB=∠BAC+
∠AOB=∠BAC+ ∠AOB,
∠AOB,∴∠C=
 ∠AOB,
∠AOB,∵∠AOB=90°,
∴∠C=45°.
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式表示出∠ABD、∠ABP,再根据角平分线的定义可得∠ABD=
 ∠ABP,∠BAC=
∠ABP,∠BAC= ∠BAO,然后整理即可得到∠C=
∠BAO,然后整理即可得到∠C= ∠AOB,从而得解.
∠AOB,从而得解.点评:本题考查了 三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,准确识图,找出各角度的关系是解题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 小明用下面的方法画出了45°角:作两条互相垂直的直线MN、PQ,点A、B分别是MN、PQ上任意一点,作∠ABP的平分线BD,BD的反向延长线交∠OAB的平分线于点C,则∠C就是所求的45°角.你认为对吗?请给出证明.
小明用下面的方法画出了45°角:作两条互相垂直的直线MN、PQ,点A、B分别是MN、PQ上任意一点,作∠ABP的平分线BD,BD的反向延长线交∠OAB的平分线于点C,则∠C就是所求的45°角.你认为对吗?请给出证明.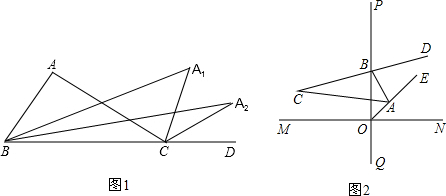

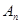 与∠
与∠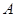 的关系式。
的关系式。