题目内容
 (2012•怀化)如图,已知AB是⊙O的弦,OB=4,∠OBC=30°,点C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD、DB.
(2012•怀化)如图,已知AB是⊙O的弦,OB=4,∠OBC=30°,点C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD、DB.(1)当∠ADC=18°时,求∠DOB的度数;
(2)若AC=2
| 3 |
分析:(1)连接OA,根据OA=OB=OD,求出∠DAO、∠OAB的度数,求出∠DAB,根据圆周角定理求出即可;
(2)过O作OE⊥AB于E,根据垂径定理求出AE和BE,求出AB,推出C、E重合,得出∠ACD=∠OCB=90°,求出DC长得出
=
,根据相似三角形的判定推出即可.
(2)过O作OE⊥AB于E,根据垂径定理求出AE和BE,求出AB,推出C、E重合,得出∠ACD=∠OCB=90°,求出DC长得出
| AC |
| OC |
| DC |
| BC |
解答: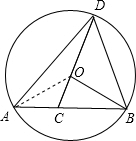 (1)解:连接OA,
(1)解:连接OA,
∵OA=OB=OD,
∴∠OAB=∠OBC=30°,∠OAD=∠ADC=18°,
∴∠DAB=∠DAO+∠BAO=48°,
由圆周角定理得:∠DOB=2∠DAB=96°.
(2)证明:过O作OE⊥AB于点E,垂足为E,
∵OE过O,
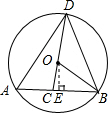 由垂径定理得:AE=BE,
由垂径定理得:AE=BE,
∵在Rt△OEB中,OB=4,∠OBC=30°,
∴OE=
OB=2,
由勾股定理得:BE=2
=AE,
即AB=2AE=4
,
∵AC=2
,
∴BC=2
,
即C、E两点重合,
∴DC⊥AB,
∴∠DCA=∠OCB=90°,
∵DC=OD+OC=2+4=6,OC=2,AC=BC=2
,
∴
=
=
,
∴△ACD∽△OCB(两边对应成比例,且夹角相等的两三角形相似).
 (1)解:连接OA,
(1)解:连接OA,∵OA=OB=OD,
∴∠OAB=∠OBC=30°,∠OAD=∠ADC=18°,
∴∠DAB=∠DAO+∠BAO=48°,
由圆周角定理得:∠DOB=2∠DAB=96°.
(2)证明:过O作OE⊥AB于点E,垂足为E,
∵OE过O,
 由垂径定理得:AE=BE,
由垂径定理得:AE=BE,∵在Rt△OEB中,OB=4,∠OBC=30°,
∴OE=
| 1 |
| 2 |
由勾股定理得:BE=2
| 3 |
即AB=2AE=4
| 3 |
∵AC=2
| 3 |
∴BC=2
| 3 |
即C、E两点重合,
∴DC⊥AB,
∴∠DCA=∠OCB=90°,
∵DC=OD+OC=2+4=6,OC=2,AC=BC=2
| 3 |
∴
| AC |
| OC |
| CD |
| BC |
| 3 |
∴△ACD∽△OCB(两边对应成比例,且夹角相等的两三角形相似).
点评:本题综合考查了垂径定理,圆周角定理,相似三角形的判定,勾股定理,等腰三角形的性质的应用,主要考查学生能否运用性质进行推理,题目综合性比较强,是一道比较好的题目.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 (2012•怀化)如图,已知AB∥CD,AE平分∠CAB,且交于点D,∠C=110°,则∠EAB为( )
(2012•怀化)如图,已知AB∥CD,AE平分∠CAB,且交于点D,∠C=110°,则∠EAB为( ) (2012•怀化)如图,点P是⊙O外一点,PA是⊙O的切线,切点为A,⊙O的半径OA=2cm,∠P=30°,则PO=
(2012•怀化)如图,点P是⊙O外一点,PA是⊙O的切线,切点为A,⊙O的半径OA=2cm,∠P=30°,则PO=
 ⊙G,试判断直线CM与⊙G的位置关系,并说明理由.
⊙G,试判断直线CM与⊙G的位置关系,并说明理由.