题目内容
(2012•怀化)如图,抛物线m:y=-
(x+h)2+k与x轴的交点为A、B,与y轴的交点为C,顶点为M(3,
),将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为D;
(1)求抛物线n的解析式;
(2)设抛物线n与x轴的另一个交点为E,点P是线段ED上一个动点(P不与E、D重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为(x,y),△PEF的面积为S,求S与x的函数关系式,写出自变量x的取值范围,并求出S的最大值;
(3)设抛物线m的对称轴与x轴的交点为G,以G为圆心,A、B两点间的距离为直径作 ⊙G,试判断直线CM与⊙G的位置关系,并说明理由.
⊙G,试判断直线CM与⊙G的位置关系,并说明理由.
| 1 |
| 4 |
| 25 |
| 4 |
(1)求抛物线n的解析式;
(2)设抛物线n与x轴的另一个交点为E,点P是线段ED上一个动点(P不与E、D重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为(x,y),△PEF的面积为S,求S与x的函数关系式,写出自变量x的取值范围,并求出S的最大值;
(3)设抛物线m的对称轴与x轴的交点为G,以G为圆心,A、B两点间的距离为直径作
 ⊙G,试判断直线CM与⊙G的位置关系,并说明理由.
⊙G,试判断直线CM与⊙G的位置关系,并说明理由.分析:(1)本问涉及抛物线的旋转变换,首先求出B点坐标,再由点D、M关于点B成中心对称,求出D点的坐标,从而得到抛物线n的解析式;注意由于开口方向相反,两个抛物线的a值也相反;
(2)本问可依次确定S的关系式、自变量x的取值范围,最后求出最大值.注意:①欲求S的关系式,首先需要用待定系数法求出直线DE的解析式;②求得关系式S=-
(x-9)2+
后确定最大值时,不能简单套用“当x=9时,最大值为…”,这样就错了,因为x=9不在自变量的取值范围内;
(3)本问结论:直线CM与⊙G相切.结合题意,欲证明直线CM与⊙G相切,需要完成两个步骤:①证明点C在⊙G上,②证明CM垂直于半径GC.
(2)本问可依次确定S的关系式、自变量x的取值范围,最后求出最大值.注意:①欲求S的关系式,首先需要用待定系数法求出直线DE的解析式;②求得关系式S=-
| 5 |
| 8 |
| 405 |
| 8 |
(3)本问结论:直线CM与⊙G相切.结合题意,欲证明直线CM与⊙G相切,需要完成两个步骤:①证明点C在⊙G上,②证明CM垂直于半径GC.
解答:解:(1)依题意,抛物线m的解析式为:y=-
(x-3)2+
=-
(x-8)(x+2),
∴A(-2,0),B(8,0).
由旋转性质可知,点D与点M(3,
)关于点B(8,0)成中心对称,
∴D(13,-
),
∴抛物线n的解析式为:y=
(x-13)2-
.
(2)∵抛物线n:y=
(x-13)2-
=
(x-8)(x-18),∴E点坐标为(18,0).
设直线DE的解析式为y=kx+b,则有:
,解得k=
,b=-
,
∴直线DE的解析式为:y=
x-
.
如题图所示,S=
PF•OF=
x•(-y)=-
x•(
x-
)=-
(x-9)2+
;
∵点P是线段ED上一个动点(P不与E、D重合),∴13<x<18;
∴S=-
(x-9)2+
(13<x<18),
可见该抛物线开口向下,对称轴为x=9,函数图象位于对称轴右侧,y随着x的增大而减小,故S在13<x<18范围内没有最大值.
所以S与x的函数关系式为S=-
(x-9)2+
,自变量取值范围是13<x<18,S没有最大值.
(3)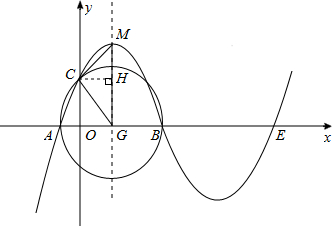 结论:直线CM与⊙G相切.理由如下:
结论:直线CM与⊙G相切.理由如下:
∵抛物线m的解析式为:y=-
(x-3)2+
,令x=0,解得y=4,∴C(0,4).
在Rt△COG中,由勾股定理得:CG=
=
=5,
又∵⊙G半径为5,∴点C在⊙G上.
如右图所示,依题意作出⊙G,连接CG、CM、MG,过点C作CH⊥MG于点H,则CH=3,HG=4,MH=
-4=
,
∵
=
=
,CH⊥MG,
∴△CHG∽△MHC,∴∠MCH=∠CGH;
又∠HCG+∠CGH=90°,∴∠HCG+∠MCH=90°,即GC⊥MC.
(注:此处亦可用勾股定理的逆定理证明△MCG为直角三角形)
综上所述,点C在⊙G上,且满足GC⊥MC,
∴直线CM与与⊙G相切.
| 1 |
| 4 |
| 25 |
| 4 |
| 1 |
| 4 |
∴A(-2,0),B(8,0).
由旋转性质可知,点D与点M(3,
| 25 |
| 4 |
∴D(13,-
| 25 |
| 4 |
∴抛物线n的解析式为:y=
| 1 |
| 4 |
| 25 |
| 4 |
(2)∵抛物线n:y=
| 1 |
| 4 |
| 25 |
| 4 |
| 1 |
| 4 |
设直线DE的解析式为y=kx+b,则有:
|
| 5 |
| 4 |
| 45 |
| 2 |
∴直线DE的解析式为:y=
| 5 |
| 4 |
| 45 |
| 2 |
如题图所示,S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 45 |
| 2 |
| 5 |
| 8 |
| 405 |
| 8 |
∵点P是线段ED上一个动点(P不与E、D重合),∴13<x<18;
∴S=-
| 5 |
| 8 |
| 405 |
| 8 |
可见该抛物线开口向下,对称轴为x=9,函数图象位于对称轴右侧,y随着x的增大而减小,故S在13<x<18范围内没有最大值.
所以S与x的函数关系式为S=-
| 5 |
| 8 |
| 405 |
| 8 |
(3)
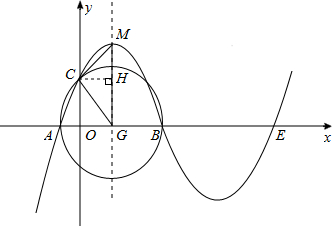 结论:直线CM与⊙G相切.理由如下:
结论:直线CM与⊙G相切.理由如下:∵抛物线m的解析式为:y=-
| 1 |
| 4 |
| 25 |
| 4 |
在Rt△COG中,由勾股定理得:CG=
| OG2+OC2 |
| 32+42 |
又∵⊙G半径为5,∴点C在⊙G上.
如右图所示,依题意作出⊙G,连接CG、CM、MG,过点C作CH⊥MG于点H,则CH=3,HG=4,MH=
| 25 |
| 4 |
| 9 |
| 4 |
∵
| CH |
| HG |
| MH |
| CH |
| 3 |
| 4 |
∴△CHG∽△MHC,∴∠MCH=∠CGH;
又∠HCG+∠CGH=90°,∴∠HCG+∠MCH=90°,即GC⊥MC.
(注:此处亦可用勾股定理的逆定理证明△MCG为直角三角形)
综上所述,点C在⊙G上,且满足GC⊥MC,
∴直线CM与与⊙G相切.
点评:本题综合考查了二次函数的图象与性质、图形变换、极值、相似三角形的判定与性质、勾股定理以及圆与直线的位置关系等知识点,有一定的难度.第(2)问中,考查二次函数在指定区间上的极值,这是本题的一个易错点,需要引起注意.

练习册系列答案
相关题目
 (2012•怀化)如图,已知AB∥CD,AE平分∠CAB,且交于点D,∠C=110°,则∠EAB为( )
(2012•怀化)如图,已知AB∥CD,AE平分∠CAB,且交于点D,∠C=110°,则∠EAB为( ) (2012•怀化)如图,点P是⊙O外一点,PA是⊙O的切线,切点为A,⊙O的半径OA=2cm,∠P=30°,则PO=
(2012•怀化)如图,点P是⊙O外一点,PA是⊙O的切线,切点为A,⊙O的半径OA=2cm,∠P=30°,则PO= (2012•怀化)如图,已知AB是⊙O的弦,OB=4,∠OBC=30°,点C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD、DB.
(2012•怀化)如图,已知AB是⊙O的弦,OB=4,∠OBC=30°,点C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD、DB.