题目内容
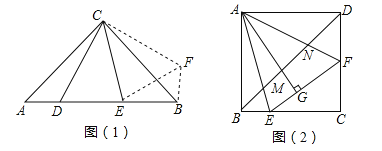
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.

(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
【答案】(1)证明见解析;(2)①△ACE是直角三角形;②a:b=![]() :1,∠AEC=45°.
:1,∠AEC=45°.
【解析】
试题分析:(1)根据正方形的性质和全等三角形的判定定理证明△APE≌△CFE,根据全等三角形的性质证明结论;
(2)①根据正方形的性质、等腰直角三角形的性质解答;
②根据PE∥CF,得到![]() ,代入a、b的值计算求出a:b,根据角平分线的判定定理得到∠HCG=∠BCG,证明∠AEC=∠ACB,即可求出∠AEC的度数.
,代入a、b的值计算求出a:b,根据角平分线的判定定理得到∠HCG=∠BCG,证明∠AEC=∠ACB,即可求出∠AEC的度数.
试题解析:(1)∵四边形ABCD和四边形BPEF是正方形,∴AB=BC,BP=BF,∴AP=CF,在△APE和△CFE中,∵AP=CF,∠P=∠F,PE=EF,∴△APE≌△CFE,∴EA=EC;
(2)①∵P为AB的中点,∴PA=PB,又PB=PE,∴PA=PE,∴∠PAE=45°,又∠DAC=45°,∴∠CAE=90°,即△ACE是直角三角形;
②∵EP平分∠AEC,EP⊥AG,∴AP=PG=a﹣b,BG=a﹣(2a﹣2b)=2b﹣a
∵PE∥CF,∴![]() ,即
,即![]() ,解得:
,解得:![]() ;
;
作GH⊥AC于H,∵∠CAB=45°,∴HG=![]() AG=
AG=![]() =
=![]() ,又BG=2b﹣a=
,又BG=2b﹣a=![]() ,∴GH=GB,GH⊥AC,GB⊥BC,∴∠HCG=∠BCG,∵PE∥CF,∴∠PEG=∠BCG,∴∠AEC=∠ACB=45°,∴a:b=
,∴GH=GB,GH⊥AC,GB⊥BC,∴∠HCG=∠BCG,∵PE∥CF,∴∠PEG=∠BCG,∴∠AEC=∠ACB=45°,∴a:b=![]() :1;∴∠AEC=45°.
:1;∴∠AEC=45°.

练习册系列答案
相关题目