Question

【题目】两个三角板ABC，DEF，按如图所示的位置摆放，点B与点D重合，边AB与边DE在同一条直线上（假设图形中所有的点，线都在同一平面内），其中，∠C=∠DEF=90°，∠ABC=∠F=30°，AC=DE=6cm.现固定三角板DEF，将三角板ABC沿射线DE方向平移，当点C落在边EF上时停止运动.设三角板平移的距离为x(cm)，两个三角板重叠部分的面积为y(cm2).

(1)当点C落在边EF上时，x=_____cm；

(2)若两个三角板重叠部分的图形为四边形时，求y关于x的函数解析式，并写出自变量x的取值范围；

(3)设边BC的中点为点M，边DF的中点为点N，直接写出在三角板平移过程中，点M与点N之间距离的最小值.

Answer 1

【答案】（１）15；（2）①y=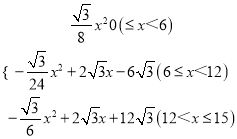；（3）

【解析】试题分析：（1）根据锐角三角函数，可得BG的长，根据线段的和差，可得GE的长，根据矩形的性质，可得答案；（2）分类讨论：①当0≤t＜6时，根据三角形的面积公式，可得答案；②当6≤t＜12时，③当12＜t≤15时，根据面积的和差，可得答案；（3）根据点与直线上所有点的连线中垂线段最短，可得M在线段NG上，根据三角形的中位线，可得NG的长，根据锐角三角函数，可得MG的长，根据线段的和差，可得答案；

试题解析：

（1）如图1所示：作CG⊥AB于G点．，

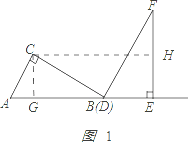
在Rt△ABC中，由AC=6，∠ABC=30，得

BC==6．

在Rt△BCG中，BG=BCcos30°=9．

四边形CGEH是矩形，

CH=GE=BG+BE=9+6=15cm，

（2）①当0≤x＜6时，如图2所示．

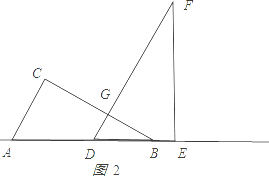
∠GDB=60°，∠GBD=30°，DB=x，得

DG=x，BG=x，重叠部分的面积为y=DGBG=×x×x=x2

②当6≤x＜12时，如图3所示：

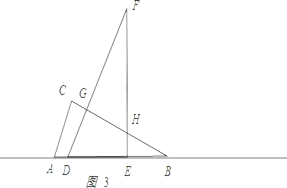
BD=x，DG=x，BG=x，BE=x﹣6，EH=（x﹣6）．

重叠部分的面积为y=S△BDG﹣S△BEH=DGBG﹣BEEH，

即y=×x×x﹣（x﹣6）（x﹣6）

化简，得y=﹣x2+2x﹣6；

③当12＜x≤15时，如图4所示：

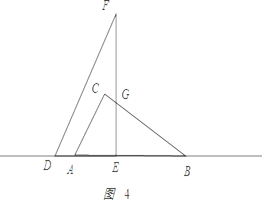
AC=6，BC=6，BD=x，BE=（x﹣6），EG=（x﹣6），

重叠部分的面积为y=S△ABC﹣S△BEG=ACBC﹣BEEG，

即y=×6×6﹣（x﹣6）（x﹣6），

化简，得y=18﹣（x2﹣12x+36）=﹣x2+2x+12；

综上所述：y=；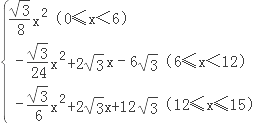

（3）如图5所示作NG⊥DE于G点．，

点M在NG上时MN最短，

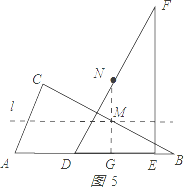
NG是△DEF的中位线，

NG=EF=．

MB=CB=3，∠B=30°，

MG=MB=，

MN最小=3﹣=。