Question

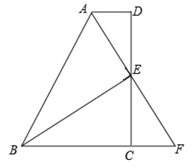
【题目】如图，在四边形中， ， 、分别是、的中点．

（）求证： ．

（）若，求的度数．

Answer 1

【答案】（1）见解析；（2）

【解析】试题分析：（1）首先由直接三角形的斜边上的中线的性质得出AM＝CM，进一步利用等腰三角形的三线合一得出结论；

（2）由直接三角形的斜边上的中线的性质得出AM＝MD＝MC，利用三角形的内角和得出∠AMD＝180°－2∠ADM，∠CMD＝180°－2∠CDM，求得∠AMC，进一步利用等腰三角形的性质得出答案即可．

试题解析：

（）证明：∵M为BD中点，

在Rt△ABD中，AM＝BD，

在Rt△BCD中，CM＝BD，

∴AM＝CM，

∴△AMC为等腰三角形，

∵N为AC中点，

∴MN⊥AC．

（）解：∵M是BD的中点，

∴MD＝BD，

∴AM＝DM，

∴∠AMD＝180°－2∠ADM，

同理∠CMD＝180°－2∠CDM，

∴∠AMC＝∠AMD＋∠CMD＝180°－2∠ADM＋180°－2∠CDM＝120°，

∵AM＝DM，

∴∠1＝∠2＝30°．