题目内容
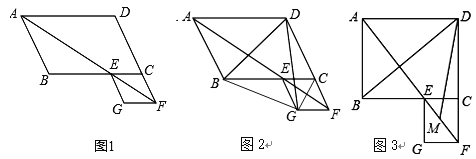
【题目】在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作□ECFG.
(1)如图1,证明□ECFG为菱形;
(2)如图2,若∠ABC=120°,连接BG、CG,求证△DGC≌△BGE,并求出∠BDG的度数;
(3)如图3,若∠ABC=90°,M是EF的中点,请直接写出∠BDM的度数.
【答案】(1)证明见解析;(2)∠BDG=60°;(3)∠BDM=45°
【解析】分析:(1)平行四边形的性质可得AD∥BC,AB∥CD,再根据平行线的性质证明∠CEF=∠CFE,根据等角对等边可得CE=CF,再有条件四边形ECFG是平行四边形,可得四边形ECFG为菱形;
(2)延长AB、FG交于H,连接HD,求证平行四边形AHFD为菱形,得出△ADH,△DHF为全等的等边三角形,证明△BHD≌△GFD,即可得出答案;
(3)首先证明四边形ECFG为正方形,再证明△BME≌△DMC可得DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到∠BDM的度数.
解:(1)证明:∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴□ECFG为菱形.
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD

∴∠BAD+∠ABC=180°,∠BCF=∠ABC,∠DAF=∠AEB,
∵∠ABC=120°,
∴∠BAD=60°,∠BCF=120°,
∵AF平分∠BAD,
∴∠BAF=∠DAE=30°,
∴∠BAF=∠BEA=30°,
∴AB=BE,
∴BE=CD,
∵四边形ECFG为菱形,且∠BCF=120°
∴△ECG,△GCF为全等的等边三角形,
∴GE=GC,∠GEC=∠GCE=60°,
∴∠BEG=∠DCG=120°,
∴△DGC≌△BGE(SAS),
∴∠BGE=∠DGC,BG=DG
∴∠BGD=∠BGE+∠EGD=∠DGC+∠EGD=60°,
∴△BGD是等边三角形,
∴∠BDG=60°;
(3)如图2,∠BDM=45°;

如图,连接BM,MC,
∵∠ABC=90,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形,
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵ ,
,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形,
∴∠BDM=45°.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案