题目内容
如图,BD、CE为⊿ABC的高,求证⊿AED=⊿ACB.
先证⊿ABD∽⊿ACE可得AE:AD=AC:AB,加上∠A=∠A可证⊿ADE∽⊿ABC得⊿AED=⊿ACB
解析考点:相似三角形的判定与性质.
分析:要证∠AED=∠ACB,只要证△ADE∽△ABC,要证全等,有∠A=∠A,只要有 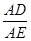 =
= 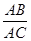 就可,要证
就可,要证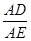 =
= 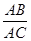 成立,只要△ABD∽△ACE就可,根据已知条件:BD、CE为△ABC的高,又∠A=∠A可证明结论.
成立,只要△ABD∽△ACE就可,根据已知条件:BD、CE为△ABC的高,又∠A=∠A可证明结论.
证明:∵∠ADB=∠AEC=90°,∠A=∠A,
∴△ABD∽△ACE.
∴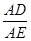 =
= 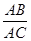 .
.
又∠A=∠A,
∴△ADE∽△ABC.
∴∠AED=∠ACB.

练习册系列答案
相关题目
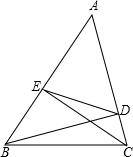 如图,BD、CE为△ABC的高,求证:∠AED=∠ACB.
如图,BD、CE为△ABC的高,求证:∠AED=∠ACB.