题目内容
【题目】如图,在△ABC中,AB=10,BC=12,BC边上的中线AD=8. 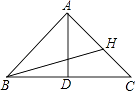
(1)证明:△ABC为等腰三角形;
(2)点H在线段AC上,试求AH+BH+CH的最小值.
【答案】
(1)解:∵AD是BC边上的中线,
∴BD=DC=6.
在△ABD中,BD2+AD2=62+82=102=AB2,
∴△ABD为直角三角形.
∴∠ADB=90°.
∴AD⊥BC.
∵AD⊥BC,BD=DC,
∴AB=AC.
∴△ABC为等腰三角形.
(2)解:∵AH+BH+CH=AC+BH=10+BH,
∴当BH最小时,AH+BH+CH有最小值.
由垂线段的性质可知当BH⊥AC时,BH有最小值.
∴ ![]() BHAC=
BHAC= ![]() BCAD,即
BCAD,即 ![]() ×10BH=
×10BH= ![]() ×12×8,
×12×8,
解得:BH=9.6.
∴AH+BH+CH的最小值=10+9.6=19.6.
【解析】(1)由三角形的中线的定义可知BD=DC=6,然后依据勾股定理的逆定理可证明△ABD为直角三角形,故此AD⊥BC,则AD为BC的垂直平分线,依据线段垂直平分线的性质可知AB=AC;(2)由题意可得到CH+AC=AC=10,故此当BH最小时,AH+BH+CH有最小值,依据垂线段的性质可知当BH⊥AC时,BH有最小值,在△ABC中,依据面积法可求得BH的最小值.

练习册系列答案
相关题目