题目内容
【题目】如图，一段抛物线y=﹣x（x﹣3）（0≤x≤3），记为C1 ， 它与x轴交于点O，A1；将C1绕点A1旋转180°得C2 ， 交x 轴于点A2；将C2绕点A2旋转180°得C3 ， 交x 轴于点A3；…如此进行下去，得到一条“波浪线”．若点P（37，m）在此“波浪线”上，则m的值为 ．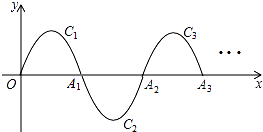 
【答案】2
【解析】解：∵一段抛物线：y=﹣x（x﹣3）（0≤x≤3），
∴图象与x轴交点坐标为：（0，0），（3，0），
∵将C1绕点A1旋转180°得C2，交x轴于点A2；
将C2绕点A2旋转180°得C3，交x轴于点A3；
…
如此进行下去，直至得C13．
∴C13的解析式与x轴的交点坐标为（36，0），（39，0），且图象在x轴上方，
∴C13的解析式为：y13=﹣（x﹣36）（x﹣39），
当x=37时，y=﹣（37﹣36）×（37﹣39）=2．
所以答案是：2．
【考点精析】本题主要考查了二次函数图象的平移的相关知识点，需要掌握平移步骤：（1）配方 y=a(x-h)2+k，确定顶点（h,k）（2）对x轴左加右减；对y轴上加下减才能正确解答此题．
练习册系列答案
相关题目
【题目】如图，数轴上一动点
从原点出发，在数轴上进行往返运动，运动情况如下表（注：表格中的
表示2到4之间的数）.
运动次数 | 运动方向 | 运动路程 | 数轴上对应的数 |
第1次 | _________ | 3 | -3 |
第2次 | 左 |
| _________ |
第3次 | _________ | _________ |
|
回答下列问题：
（1）完成表格；
（2）已知第4次运动的路程为
.
①此时数轴上对应的数是_________；
②若第4次运动后点恰好回到原点，则这4次运动的总路程是多少？
