题目内容
(2003•天津)已知,如图⊙O1与⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点.(1)求证:AB⊥AC;
(2)若r1、r2分别为⊙O1、⊙O2的半径,且r1=2r2.求
 的值.
的值.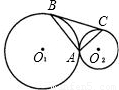
【答案】分析:(1)过点A作两圆的内公切线交BC于点O,再利用切线的性质,证明OA=OB=OC即可;
(2)连续OO1、OO2与AB、AC分别交于点E、F,先利用切线的性质证明四边形OEAF是矩形;
再利用三角形的形似、直角三角形的特点和三角函数求出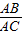 的值.
的值.
解答: (1)证明:过点A作两圆的内公切线交BC于点O.
(1)证明:过点A作两圆的内公切线交BC于点O.
∵OA、OB是⊙O1的切线,
∴OA=OB.
同理OA=OC,
∴OA=OB=OC.
于是△BAC是直角三角形,∠BAC=90°,
所以AB⊥AC.
(2)解:连接OO1、OO2与AB、AC分别交于点E、F.
∵OA、OB是⊙O1的切线.
∴OO1⊥AB,
同理OO2⊥AC.
根据(1)的结论AB⊥AC,可知四边形OEAF是矩形,有∠EOF=90°.
连接O1O2,有OA⊥O1O2.在Rt△O1OO2中,有Rt△O1AO∽Rt△OAO2,
∴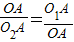 ,
,
于是OA2=O1A•O2A=r1•r2=2r22,
∴OA= r2,
r2,
又∵∠ACB是⊙O2的弦切角,
∴∠ACB=∠AO2O.
在Rt△OAO2中,tan∠AO2O=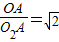 ,
,
∴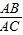 =tan∠ACB=tan∠AO2O=
=tan∠ACB=tan∠AO2O= .
.
点评:本题综合考查了直线与圆、圆与圆的位置关系,全等三角形的判定、图形的平移变换等多个知识点.
(2)连续OO1、OO2与AB、AC分别交于点E、F,先利用切线的性质证明四边形OEAF是矩形;
再利用三角形的形似、直角三角形的特点和三角函数求出
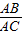 的值.
的值.解答:
 (1)证明:过点A作两圆的内公切线交BC于点O.
(1)证明:过点A作两圆的内公切线交BC于点O.∵OA、OB是⊙O1的切线,
∴OA=OB.
同理OA=OC,
∴OA=OB=OC.
于是△BAC是直角三角形,∠BAC=90°,
所以AB⊥AC.
(2)解:连接OO1、OO2与AB、AC分别交于点E、F.
∵OA、OB是⊙O1的切线.
∴OO1⊥AB,
同理OO2⊥AC.
根据(1)的结论AB⊥AC,可知四边形OEAF是矩形,有∠EOF=90°.
连接O1O2,有OA⊥O1O2.在Rt△O1OO2中,有Rt△O1AO∽Rt△OAO2,
∴
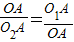 ,
,于是OA2=O1A•O2A=r1•r2=2r22,
∴OA=
 r2,
r2,又∵∠ACB是⊙O2的弦切角,
∴∠ACB=∠AO2O.
在Rt△OAO2中,tan∠AO2O=
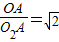 ,
,∴
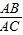 =tan∠ACB=tan∠AO2O=
=tan∠ACB=tan∠AO2O= .
.点评:本题综合考查了直线与圆、圆与圆的位置关系,全等三角形的判定、图形的平移变换等多个知识点.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 ,1),C(1,1),问是否存在点M,使p+q=
,1),C(1,1),问是否存在点M,使p+q= ?若存在,求出点M的坐标;若不存在,请说明理由.
?若存在,求出点M的坐标;若不存在,请说明理由.