题目内容
平面上有9条直线，任意两条都不平行，欲使它们出现29个交点，能否做到，如果能，怎么安排才能做到？如果不能，请说明理由．分析：根据相交线最多交点的个数的公式
进行计算即可求解．
| n(n-1) |
| 2 |
解答：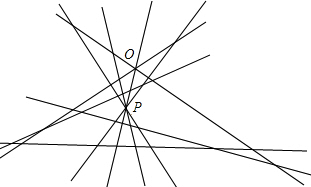
解：能．理由如下：
9条直线，任意两条都不平行，最多交点的个数是
=
=36，
∵36＞29，
∴能出现29个交点，
安排如下：先使4条直线相交于一点P，另外5条直线两两相交最多可得
=10个交点，
与前四条直线相交最多可得5×4=20个交点，
让其中两个点重合为点O，所以交点减少1个，
交点个数一共有10+20-1=29个．
故能做到．
解：能．理由如下：9条直线，任意两条都不平行，最多交点的个数是
| n(n-1) |
| 2 |
| 9×8 |
| 2 |
∵36＞29，
∴能出现29个交点，
安排如下：先使4条直线相交于一点P，另外5条直线两两相交最多可得
| 5×(5-1) |
| 2 |
与前四条直线相交最多可得5×4=20个交点，
让其中两个点重合为点O，所以交点减少1个，
交点个数一共有10+20-1=29个．
故能做到．
点评：本题考查了相交线的问题，熟记最多交点的公式然后求出最多时的交点个数是解题的关键．
练习册系列答案
相关题目
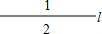（1）一条直线可以把平面分成两个部分（或区域），如图，两条直线可以把平面分成几个部分？三条直线可以把平面分成几个部分？试画图说明．