题目内容
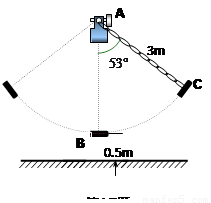
 16、如图所示,秋千链子的长度为3m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为53°,则秋千踏板与地面的最大距离约为多少?
16、如图所示,秋千链子的长度为3m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为53°,则秋千踏板与地面的最大距离约为多少?(参考数据:sin53°≈0.8,cos53°≈0.6)
分析:如图所示,在△ABC中,BC⊥AC,AB=3,∠CAB=53°,故有AC=3cos53°≈3×0.6=1.8,CD≈3+0.5-1.8=1.7,即BE=CD=1.7m.
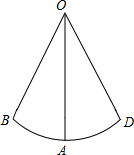
解答: 解:设秋千链子的上端固定于A处,秋千踏板摆动到最高位置时踏板位于B处.过点A,B的铅垂线分别为AD,BE,点D,E在地面上,过B作BC⊥AD于点C.
解:设秋千链子的上端固定于A处,秋千踏板摆动到最高位置时踏板位于B处.过点A,B的铅垂线分别为AD,BE,点D,E在地面上,过B作BC⊥AD于点C.
在Rt△ABC中,AB=3,∠CAB=53°,
∴AC=3cos53°≈3×0.6=1.8(m),
∴CD≈3+0.5-1.8=1.7(m),
∴BE=CD≈1.7(m),
答:秋千摆动时踏板与地面的最大距离约为1.7m.
 解:设秋千链子的上端固定于A处,秋千踏板摆动到最高位置时踏板位于B处.过点A,B的铅垂线分别为AD,BE,点D,E在地面上,过B作BC⊥AD于点C.
解:设秋千链子的上端固定于A处,秋千踏板摆动到最高位置时踏板位于B处.过点A,B的铅垂线分别为AD,BE,点D,E在地面上,过B作BC⊥AD于点C.在Rt△ABC中,AB=3,∠CAB=53°,
∴AC=3cos53°≈3×0.6=1.8(m),
∴CD≈3+0.5-1.8=1.7(m),
∴BE=CD≈1.7(m),
答:秋千摆动时踏板与地面的最大距离约为1.7m.
点评:解此题的关键是把实际问题转化为数学问题,只要把实际问题抽象到解直角三角形中,利用三角函数即可解答.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目


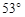 ,则秋千踏板与地面的最大距离约为多少?(参考数据:
,则秋千踏板与地面的最大距离约为多少?(参考数据: ≈0.8,
≈0.8, 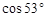 ≈0.6)
≈0.6)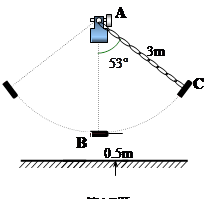
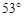 ,则秋千踏板与地面的最大距离约为多少?(参考数据:
,则秋千踏板与地面的最大距离约为多少?(参考数据: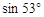 ≈0.8,
≈0.8,
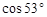 ≈0.6)
≈0.6)