题目内容
已知⊙O1与⊙O2相切于点P,它们的半径分别为R、r.一直线绕P点旋转,与⊙O1、⊙O2分别交于点A、B(点P、B不重合),探索规律:(1)如图1,当⊙O1与⊙O2外切时,探求
| PA | PB |
(2)如图2,当⊙O1与⊙O2内切时,第(1)题探求
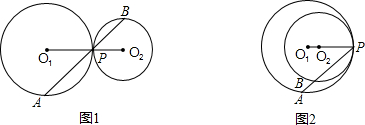 的结论是否成立?为什么?
的结论是否成立?为什么?
分析:要求
与半径R、r之间的关系式,证明△O1AP∽△O2BP是关键,注意两圆的位置关系.
| PA |
| PB |
解答: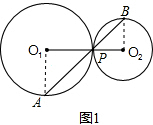 解:(1)当⊙O1与⊙O2外切时,
解:(1)当⊙O1与⊙O2外切时,
=
(3分)
证明:连接O1A,O2B
∵两圆外切,
∴O1、P、O2三点共线
∵△O1AP和△O2BP是等腰三角形,∠O1PA=∠BPO2,
∴∠O1AP=∠O2BP
∴△O1AP∽△O2BP
∴
=
;(4分)
(2)当⊙O1与⊙O2内切时,
=
仍然成立(2分)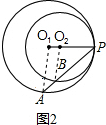
证明:连接O1A,O2B,同理可证△PO1A∽△PO2B,
∴
=
仍然成立.(3分)
(注:能指出当动直线AB经过两圆的圆心时,PA=2R,PB=2r,∴
=
,奖励1分.)
 解:(1)当⊙O1与⊙O2外切时,
解:(1)当⊙O1与⊙O2外切时,| PA |
| PB |
| R |
| r |
证明:连接O1A,O2B
∵两圆外切,
∴O1、P、O2三点共线
∵△O1AP和△O2BP是等腰三角形,∠O1PA=∠BPO2,
∴∠O1AP=∠O2BP
∴△O1AP∽△O2BP
∴
| PA |
| PB |
| R |
| r |
(2)当⊙O1与⊙O2内切时,
| PA |
| PB |
| R |
| r |

证明:连接O1A,O2B,同理可证△PO1A∽△PO2B,
∴
| PA |
| PB |
| R |
| r |
(注:能指出当动直线AB经过两圆的圆心时,PA=2R,PB=2r,∴
| PA |
| PB |
| R |
| r |
点评:本题考查了两圆的位置关系,相似三角形的判定和性质,是一个探究性的题目.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目