题目内容
若方程(x2-1)(x2-4)=k有四个非零实根,且它们在数轴上对应的四个点等距排列,则k= .
【答案】分析:设x2=y,原方程变为y2-5y+(4-k)=0,设此方程有实根α,β(0<α<β),根据根与系数的关系即可求出k的值.
解答:解:设x2=y,原方程变为y2-5y+(4-k)=0,
设此方程有实根α,β(0<α<β),
则原方程的四个实根为±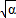 ,±
,±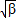 ,
,
由于它们在数轴上等距排列,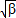 -
-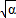 =
=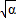 -(-
-(-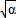 )
)
即β=9α,①又 α+β=5,αβ=4-k,
由此求得k= 且满足△=25+4k-16>0,∴k=
且满足△=25+4k-16>0,∴k= .
.
故答案为: .
.
点评:本题考查了解高次方程,难度一般,关键是用换元法求解方程.
解答:解:设x2=y,原方程变为y2-5y+(4-k)=0,
设此方程有实根α,β(0<α<β),
则原方程的四个实根为±
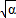 ,±
,±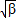 ,
,由于它们在数轴上等距排列,
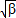 -
-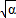 =
=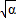 -(-
-(-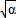 )
)即β=9α,①又 α+β=5,αβ=4-k,
由此求得k=
 且满足△=25+4k-16>0,∴k=
且满足△=25+4k-16>0,∴k= .
.故答案为:
 .
.点评:本题考查了解高次方程,难度一般,关键是用换元法求解方程.

练习册系列答案
相关题目
若方程:x2+2x-1=0的两根为x1、x2,则代数式:
+
的值为( )
| x2 |
| x1 |
| x1 |
| x2 |
| A、-6 | B、2 | C、-4 | D、-2 |