题目内容
【题目】在△ABC中,AB、BC的垂直平分线相交于三角形内一点O,下列结论中,错误的是( )
A. 点O在AC的垂直平分线上
B. △AOB、△BOC、△COA都是等腰三角形
C. ∠OAB+∠OBC+∠OCA=90°
D. 点O到AB、BC、CA的距离相等
【答案】D
【解析】试题分析:根据垂直平分线的性质得:O也是AC垂直平分线上的点,则O到三个顶点的距离相等,可以得△AOB、△BOC、△COA都是等腰三角形,且根据等边对等角得:∠OAB=∠ABO,∠OBC=∠OCB,∠OAC=∠OCA,再由三角形内角和定理得:∠OAB+∠OBC+∠OCA=90°;
三角形的角平分线的交点到三边的距离相等.
解:A、连接AO、BO、CO,
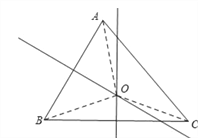
∵AB、BC的垂直平分线相交于三角形内一点O,
∴AO=BO,BO=CO,
∴AO=CO,
∴点O在AC的垂直平分线上,
所以选项A正确;
B、∵AO=BO,BO=CO,AO=CO,
∴△AOB、△BOC、△COA都是等腰三角形,
所以选项B正确;
C、∵AO=BO,BO=CO,AO=CO,
∴∠OAB=∠ABO,∠OBC=∠OCB,∠OAC=∠OCA,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠OAB+∠OBC+∠OCA=90°,
故选项C正确;
D、∵点O是三边垂直平分线的交点,
∴OA=OB=OC,
但点O到AB、BC、CA的距离不一定相等;
所以选项D错误;
本题选择错误的,
故选D.

练习册系列答案
相关题目

