题目内容
已知一水池中有600立方米的水，每小时放水50立方米．
（1）写出剩余水的体积Q（立方米）与时间t（小时）之间的函数关系式；
（2）写出自变量t的取值范围；
（3）8小时后池中还有多少立方米水？
（4）几小时后池中还有100立方米水？
解：（1）由已知条件知，每小时放50立方米水，
则t小时后放水50t立方米，
而水池中总共有600立方米的水，
那么经过t时后，剩余的水为600-50t，
故剩余水的体积Q立方米与时间t（时）之间的函数关系式为：Q=600-50t；
（2）由于t为时间变量，所以 t≥0
又因为当t=12时将水池的水全部抽完了．
故自变量t的取值范围为：0≤t≤12；
（3）根据（1）式，当t=8时，Q=200
故8小时后，池中还剩200立方米水；
（4）当Q=100时，根据（1）式解得 t=10．
故10小时后，池中还有100立方米的水．
分析：（1）根据函数的概念和所给的已知条件即可列出关系式；
（2）结合实际即可得出时间t的取值范围；
（3）根据（1）中的函数关系式，将t=8代入即可得出池中的水；
（4）结合已知，可知Q=100，代入函数关系式中即可得出时间t．
点评：本题考查了一次函数的应用，本题的关键是解决第一问，然后根据第一问，剩下的三个小问题代入自变量就可得出结果．
则t小时后放水50t立方米，
而水池中总共有600立方米的水，
那么经过t时后，剩余的水为600-50t，
故剩余水的体积Q立方米与时间t（时）之间的函数关系式为：Q=600-50t；
（2）由于t为时间变量，所以 t≥0
又因为当t=12时将水池的水全部抽完了．
故自变量t的取值范围为：0≤t≤12；
（3）根据（1）式，当t=8时，Q=200
故8小时后，池中还剩200立方米水；
（4）当Q=100时，根据（1）式解得 t=10．
故10小时后，池中还有100立方米的水．
分析：（1）根据函数的概念和所给的已知条件即可列出关系式；
（2）结合实际即可得出时间t的取值范围；
（3）根据（1）中的函数关系式，将t=8代入即可得出池中的水；
（4）结合已知，可知Q=100，代入函数关系式中即可得出时间t．
点评：本题考查了一次函数的应用，本题的关键是解决第一问，然后根据第一问，剩下的三个小问题代入自变量就可得出结果．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
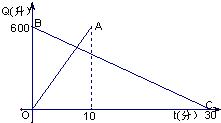28、有一个装有进出水管的容器，单位时间内进水管与出水管的进出水量均一定，已知容器的容积为600升，图中线段OA与BC，分别表示单独打开一个进水管和单独打开一个出水管时，容器的容量Q（升）随时间t（分）变化的函数关系．
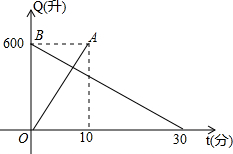开一个出水管时，容器内的水量Q（升）随时间t（分）变化的函数关系．根据图象进行以下探究：