Question

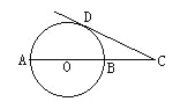
【题目】如图，AB是⊙O的直径．半径OD垂直弦AC于点E．F是BA延长线上一点，．

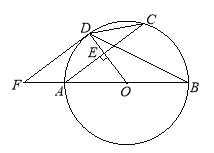
（1）判断DF与⊙O的位置关系，并证明；

（2）若AB=10，AC=8，求DF的长．

Answer 1

【答案】（1）、相切，证明过程见解析；（2）、DF=

【解析】

试题分析：（1）、根据已知条件得出∠CAB=∠BED，得到AC∥DF，根据半径OD垂直AC得到切线；（2）、根据垂径定理得出AE=4，OA=5，根据Rt△AEO的勾股定理求出OE的长度，根据AC∥DF得出△OAE∽△OFD，从而求出DF的长度.

试题解析：（1）、DF与⊙O相切．

∵∠CDB=∠CAB，又∵∠CDB=∠BFD，∴∠CAB=∠BED．

∴AC∥DF．

∵半径OD垂直于弦AC于点E，

∴OD⊥DF．

∴DF与⊙O相切．

（2）、∵半径OD垂直于弦AC于点E，AC=8，

∴AE=AC=4．∵AB是⊙O的直径，

∴OA=OD=AB=5

根据Rt△AEO的勾股定理可得：OE=3，

∵AC∥DF

∴△OAE∽△OFD

∴

即

∴DF=