Question

（2012•大连）如图，为了测量电线杆AB的高度，小明将测量仪放在与电线杆的水平距离为9m的D处．若测角仪CD的高度为1.5m，在C处测得电线杆顶端A的仰角为36°，则电线杆AB的高度约为

8.1

m．（精确到0.1m）．（参考数据sin36°≈0.59．cos36°≈0.81，tan36°≈0.73）．

Answer 1

分析：根据CE和tan36°可以求得AE的长度，根据AB=AE+EB即可求得AB的长度，即可解题．

解答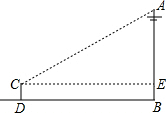：解：如图，在Rt△ACE中，
∴AE=CE•tan36°
=BD•tan36°
=9×tan36°
≈6.57米，
∴AB=AE+EB=AE+CD=6.57+1.5≈8.1（米）．
故答案为：8.1．

点评：本题考查了三角函数在直角三角形中的运用，本题中正确计算AE的值是解题的关键．