Question

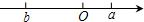如图，数轴上有两个点a、b，且|a|＜|b|，给出下列式子：①a+b；②a-b；③b-a；④ab；⑤

a

b

；⑥（a-b）³，其中结果为正的式子的个数是（　　）

• A、2个
• B、3个
• C、4个
• D、5个

Answer 1

分析：由题意，可知b＜0＜a，且|a|＜|b|，再根据有理数的加、减、乘、除、乘方的运算法则分别判断各式的符号．

解答：解：①由于b＜0＜a，且|a|＜|b|，所以a+b＜0；
②由于a＞b，则a-b＞0；
③由于a＞b，则b-a＜0；
④由于a＞0，b＜0，则ab＜0；
⑤a＞0，b＜0，则

a

b

＜0；
⑥由于a-b＞0，所以（a-b）³＞0．
则结果为正的式子共有两个．
故选A．

点评：本题借助数轴考查了有理数的加、减、乘、除、乘方的运算法则，体现了数形结合的思想．