题目内容
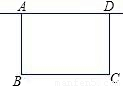
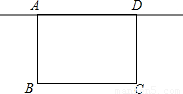
如图,学校准备在图书馆后面的场地边建一个面积为40平方米的长方形自行车棚ABCD,一边利用图书馆的后墙,设自行车棚垂直于墙的一边AB的长是x米(2≤x≤8).(1)若要利用已有总长为24米的铁围栏作为自行车的围栏,则x的值是多少?
(2)若AD=y米,求y的取值范围.
【答案】分析:(1)让周长减去2x可得AD的长,根据车棚的面积为40可得方程组,求解即可;
(2)根据(1)易得y的关系式,根据x的取值可得y的取值范围.
解答:解:(1)x(24-2x)=40
-2x2+24x=40
2x2-24x+40=0,
x2-12x+20=0,
(x-2)(x-10)=0,
解得x1=2,x2=10,
∵2≤x≤8,
∴x=2;
(2)y=24-2x,
∵2≤x≤8,
∴8≤y≤20.
点评:主要考查一元二次方程的应用;得到AD的关系式是解决本题的易错点.
(2)根据(1)易得y的关系式,根据x的取值可得y的取值范围.
解答:解:(1)x(24-2x)=40
-2x2+24x=40
2x2-24x+40=0,
x2-12x+20=0,
(x-2)(x-10)=0,
解得x1=2,x2=10,
∵2≤x≤8,
∴x=2;
(2)y=24-2x,
∵2≤x≤8,
∴8≤y≤20.
点评:主要考查一元二次方程的应用;得到AD的关系式是解决本题的易错点.

练习册系列答案
相关题目
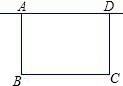 如图,学校准备在图书馆后面的场地边建一个面积为60平方米的长方形自行车棚ABCD,一边利用图书馆的后墙,设自行车棚靠墙的一边AD的长是x米(6≤x≤10).
如图,学校准备在图书馆后面的场地边建一个面积为60平方米的长方形自行车棚ABCD,一边利用图书馆的后墙,设自行车棚靠墙的一边AD的长是x米(6≤x≤10).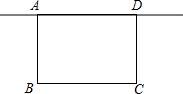 一边利用图书馆的后墙,设自行车棚垂直于墙的一边AB的长是x米(2≤x≤8).
一边利用图书馆的后墙,设自行车棚垂直于墙的一边AB的长是x米(2≤x≤8).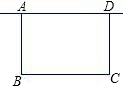 墙,设自行车棚靠墙的一边AD的长是x米(6≤x≤10).
墙,设自行车棚靠墙的一边AD的长是x米(6≤x≤10).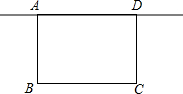 一边利用图书馆的后墙,设自行车棚垂直于墙的一边AB的长是x米(2≤x≤8).
一边利用图书馆的后墙,设自行车棚垂直于墙的一边AB的长是x米(2≤x≤8).