题目内容
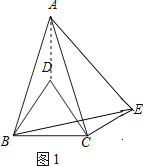
【题目】在△ABC中，AB=AC，∠BAC=α（0°＜α＜60°），分别以AB、BC为边作等边三角形ABE和等边三角形BCD，连结CE，如图1所示．
（1）直接写出∠ABD的大小（用含α的式子表示）；
（2）判断DC与CE的位置关系，并加以证明；
（3）在（2）的条件下，连结DE，如图2，若∠DEC=45°，求α的值．
【答案】（1）∠ABD=30°﹣
∠α；（2）DC与CE垂直；见解析（3）∠α=30°．
【解析】
试题分析：（1）根据等腰三角形的性质得到∠ABC=∠ACB=
=90°﹣∠α，根据角的和差即可得到结论；
（2）连接AD；根据已知条件得到∠ABD=∠EBC，推出△ABD≌△EBC，根据全等三角形的性质得到∠ADB=∠ECB，证得△ABD≌△ACD，由全等三角形的性质得到∠BAD=∠CAD=∠α，根据三角形的内角和得到∠BDA=180°﹣∠ABD﹣∠BAD=180°﹣（30°﹣∠α ）﹣∠α=150°，求得∠BCE=150°，即可得到结论．
（3）根据已知条件得到△DEC为等腰三角形，根据等腰直角三角形的性质得到DC=DE=BC，根据三角形的内角和得到∠EBC=15°，即可得到结论．
解：（1）∵AB=AC，∠A=∠α，
∴∠ABC=∠ACB=
=90°﹣∠α
∴∠ABD=∠ABC﹣∠ABE
=90°﹣∠α﹣60°
=30°﹣∠α；
（2）DC与CE垂直；
连接AD；
∵∠ABE=∠DBC=60°，
∴∠ABE﹣∠DBE=∠DBC﹣∠DBE，
即∠ABD=∠EBC，
在△ABD和△EBC中，
，
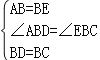∴△ABD≌△EBC，
∴∠ADB=∠ECB，
在△ABD和△ACD中，
，
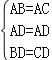∴△ABD≌△ACD，
∴∠BAD=∠CAD=
∠α，
∴∠BDA=180°﹣∠ABD﹣∠BAD=180°﹣（30°﹣∠α ）﹣∠α=150°，
∴∠BCE=150°，
∵∠BCD=60°，
∴∠DCE=90°，
即DC与CE垂直；
（3）∵∠DCE=90°，
又∵∠DEC=45°，
∴△DEC为等腰三角形，
∴DC=DE=BC，
∵∠BCE=150°，
∴∠EBC=15°，
∵∠EBC=30°﹣∠α=15°，
∴∠α=30°．
