题目内容
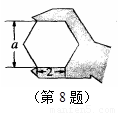
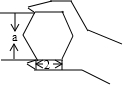如图，正六边形螺帽的边长是2cm，这个扳手的开口a的值应是分析：a的值等于正六边形的边心距的2倍，过正六边形的中心作边的垂线，连接OA，在直角△OAB中，利用三角函数求得边心距OB即可求解．
解答：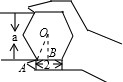
解：过正六边形的中心作边的垂线，连接OA．
则∠O=30°，AB=1
∴OB=
=
cm．
∴a=2OB=2
cm．
故答案是：2
cm．
解：过正六边形的中心作边的垂线，连接OA．则∠O=30°，AB=1
∴OB=
| AB |
| tan30° |
| 3 |
∴a=2OB=2
| 3 |
故答案是：2
| 3 |
点评：正多边形的计算基本思路是转化为解直角三角形．
练习册系列答案
相关题目
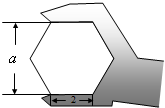如图，正六边形螺帽的边长是2cm，这个扳手的开口a的值应是（ ）A、2
| ||||
B、
| ||||
C、
| ||||
| D、1cm |
如图，正六边形螺帽的边长是2cm，这个扳手的开口a的值应是( ▲ )
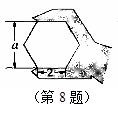
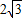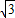| A．2cm | B．cm | C．cm | D．1cm |
cm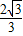
cm
cm