题目内容
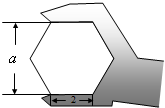 如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是( )
如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是( )A、2
| ||||
B、
| ||||
C、
| ||||
| D、1cm |
分析:连接AC,作BD⊥AC于D;根据正六边形的特点求出∠ABC的度数,再由等腰三角形的性质求出∠BAD的度数,由特殊角的三角函数值求出AD的长,进而可求出AC的长.
解答: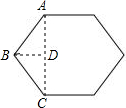 解:连接AC,过B作BD⊥AC于D;
解:连接AC,过B作BD⊥AC于D;
∵AB=BC,
∴△ABC是等腰三角形,
∴AD=CD;
∵此多边形为正六边形,
∴∠ABC=
=120°,
∴∠ABD=
=60°,
∴∠BAD=30°,AD=AB•cos30°=2×
=
,
∴a=2
cm.
故选A.
 解:连接AC,过B作BD⊥AC于D;
解:连接AC,过B作BD⊥AC于D;∵AB=BC,
∴△ABC是等腰三角形,
∴AD=CD;
∵此多边形为正六边形,
∴∠ABC=
| 180°×4 |
| 6 |
∴∠ABD=
| 120° |
| 2 |
∴∠BAD=30°,AD=AB•cos30°=2×
| ||
| 2 |
| 3 |
∴a=2
| 3 |
故选A.
点评:此题比较简单,解答此题的关键是作出辅助线,根据等腰三角形及正六边形的性质求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是( ▲ )
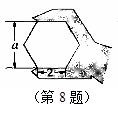

| A.2cm | B.cm | C.cm | D.1cm |
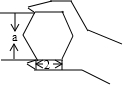 如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是
如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是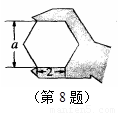

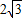 cm
cm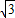 cm
cm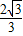 cm
cm