题目内容
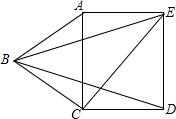如图，以等边△ABC的一边AC为边，向形外作正方形ACDE，连接BE、BD、CE，则（1）∠BCE=105°；（2）∠BAE=150°；（3）BE=BD；（4）∠DBE=30°．其中正确结论的个数是
- A.4个
- B.3个
- C.2个
- D.1个
A
分析：由等边三角形及正方形的角度，可得出（1），（2）的角度，由△ABE≌△CBD，得出线段相等，进而求出∠DBE的大小．
解答：由题意可得，∠BCE=60°+45°=105°，（1）正确；
∠BAE=90°+60°=150°，（2）正确；
（3）中∵AB=BC，AE=CD，∠BAE=∠BCD=150°，∴△ABE≌△CBD，∴BE=BD，（3）正确；
△ABE中，AB=AE，∠BAE=150°，
∴∠ABE=∠CBD=15°，
∴∠DBE=30°，（4）正确
故选A．
点评：熟练掌握正方形及等边三角形的性质，会用其性质求解一些简单的计算问题．
分析：由等边三角形及正方形的角度，可得出（1），（2）的角度，由△ABE≌△CBD，得出线段相等，进而求出∠DBE的大小．
解答：由题意可得，∠BCE=60°+45°=105°，（1）正确；
∠BAE=90°+60°=150°，（2）正确；
（3）中∵AB=BC，AE=CD，∠BAE=∠BCD=150°，∴△ABE≌△CBD，∴BE=BD，（3）正确；
△ABE中，AB=AE，∠BAE=150°，
∴∠ABE=∠CBD=15°，
∴∠DBE=30°，（4）正确
故选A．
点评：熟练掌握正方形及等边三角形的性质，会用其性质求解一些简单的计算问题．
练习册系列答案
相关题目
15、如图，以等边△ABC的一边AC为边，向形外作正方形ACDE，连接BE、BD、CE，则（1）∠BCE=105°；（2）∠BAE=150°；（3）BE=BD；（4）∠DBE=30°．其中正确结论的个数是（ ）
已知：如图，在等边△ABC中取点P，使得PA，PB，PC的长分别为3，4，5，将线段AP以点A为旋转中心顺时针旋转60°到线段AD，连接BD，下列结论：
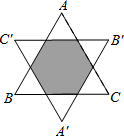如图，以等边△ABC的重心O为旋转中心，将△ABC旋转180°得到△A′B′C′，若△ABC的面积为9，则△A′B′C′与△ABC的重叠部分的面积是（ ）
如图，以等边△ABC的重心O为旋转中心，将△ABC旋转180°得到△A′B′C′，若△ABC的面积为9，则△A′B′C′与△ABC的重叠部分的面积是