题目内容
【题目】如图,⊙O为R△ABC的内切圆,⊙O的半径r=1,∠B=30°,
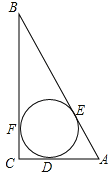
(1)劣狐DE的长。
(2)证明AD=AE。
![]() (3)求:劣狐DE、切线AD、AE所围成的面积S
(3)求:劣狐DE、切线AD、AE所围成的面积S
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() -
-![]()
![]()
【解析】
试题分析:(1)根据切线的性质得出OD⊥AC,OE⊥AB,根据四边形的内角和求得∠DOE=120°,代入公式求得即可;
(2)证明Rt△AOD≌Rt△AOE即可得到结论;
(3)根据S四边形ADOE-S扇形ODE求得即可.
试题解析:(1)∵∠B=30°
∠C=90°
∠A=60°
OD ⊥AC
OE ⊥AB
∠DOE=120°
狐DE的长=![]() =
=![]()
(2)∠AEO=∠ADO =90°
OA=OE
AO=AO
∴△AOD≌△AOE
∴AD=AE
(3) ⊙O 切AC、AB、BC于D、E 、F、
连接 OD、OE、OF、OA、OB、OC
则:OD=OE=OF=r=1
又设AC=a
∵∠B=300
∴AB=2a、 BC=![]() a
a
∴![]() ar+
ar+![]() .2ar+
.2ar+![]() .
.![]() ar=
ar=![]() a.
a.![]() a
a
(3+![]() )a=
)a=![]() a2
a2
a=1+![]()
AC = 1+![]()
四边形ODCF为正方形
CD=1
AD=![]()
S=2×![]() ×1×
×1×![]() -
-![]()
=![]() -
-![]()
![]()

练习册系列答案
相关题目