题目内容
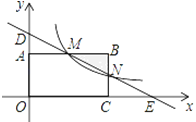
【题目】如图,在△ABC中,AB=5,AC=9,S△ABC=![]() ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
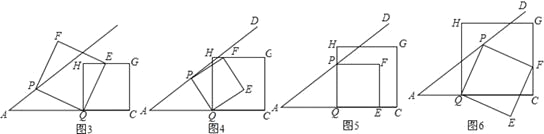
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.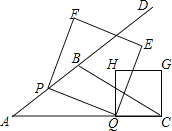
【答案】(1)![]() ;(2)S最小值=
;(2)S最小值=![]() ;(3)
;(3)![]() ;
; ![]() ;1;
;1; ![]() .
.
【解析】试题分析:(1)如图1,过点B作BM⊥AC于点M,利用面积法求得BM的长度,利用勾股定理得到AM的长度,最后由锐角三角函数的定义进行解答;
(2)如图2,过点P作PN⊥AC于点N.利用(1)中的结论和勾股定理得到PN2+NQ2=PQ2,所以由正方形的面积公式得到S关于t的二次函数,利用二次函数的顶点坐标公式和二次函数图象的性质来求其最值;
(3)需要分类讨论:当点E在边HG上、点F在边HG上、点P边QH(或点E在QC上)、点F边C上时相对应的t的值.
试题解析:(1)如图1,过点B作BM⊥AC于点M,
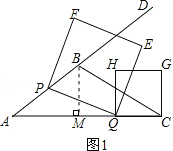
∵AC=9,S△ABC=![]() ,
,
∴![]() ACBM=
ACBM=![]() ,即
,即![]() ×9BM=
×9BM=![]() ,
,
解得BM=3.
由勾股定理,得
AM=![]() =4,
=4,
则tanA=![]() ;
;
(2)存在.如图2,过点P作PN⊥AC于点N.依题意得AP=CQ=5t.
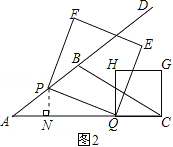
∵tanA=![]() ,
,
∴AN=4t,PN=3t.
∴QN=AC﹣AN﹣CQ=9﹣9t.
根据勾股定理得到: ![]() ,
,
S正方形PQEF= ![]() =
=![]() ﹣162t+81(0<t<
﹣162t+81(0<t<![]() ).
).
∵﹣![]() 在t的取值范围之内,
在t的取值范围之内,
∴S最小值=![]() ;
;
(3)①如图3,当点E在边HG上时,t1=![]() ;
;
②如图4,当点F在边HG上时,t2=![]() ;
;
③如图5,当点P在边QH(或点E在QC上)时,t3="1"
④如图6,当点F在边C上时,t4=![]() .
.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案